Bridging machine learning and logical reasoning by

Abductive Learning

(Press ? for help, n and p for next and previous slide)

Wang-Zhou Dai$^\dagger$

Department of Computing, Imperial College London

Joint work with Qiuling Xu$^\dagger$, Yang Yu$^\dagger$ and Zhi-Hua Zhou

Thursday Nov 28th, 2019

Motivation

Machine Learning

... now is VERY good at

Image Recognition

Speech Recognition

Mapping sensory information to a concept.

Machine Learning

... now is NOT very good at

Visual Question Answering

Learning (Simple) Relations

Machine Learning

... now is almost INCAPABLE of

QA in Context

Question: Solve -42*r + 27*c = -1167 and 130*r + 4*c = 372 for r.
Answer: 4

Question: Calculate -841880142.544 + 411127.
Answer: -841469015.544

Question: Let x(g) = 9*g + 1. Let q(c) = 2*c + 1. Let f(i) = 3*i - 39. Let w(j) = q(x(j)). Calculate f(w(a)).
Answer: 54*a - 30

Question: Let e(l) = l - 6. Is 2 a factor of both e(9) and 2?
Answer: False

Question: Let u(n) = -n**3 - n**2. Let e(c) = -2*c**3 + c. Let l(j) = -118*e(j) + 54*u(j). What is the derivative of l(a)?
Answer: 546*a**2 - 108*a - 118

Question: Three letters picked without replacement from qqqkkklkqkkk. Give prob of sequence qql.
Answer: 1/110

Do Maths in Natural Language

A Modern Rephrase of Curve Fitting

Empirical Risk Minimisation

\begin{equation} \hat{h}=\text{arg}\min_{h\in\mathcal{H}} \frac{1}{n}\sum_{i=1}^n \text{Loss}(h(\mathbf{x}_i),y_i) \end{equation}

Combine Learning and Relational Reasoning

Symbolic

Inductive Logic Programming
Statistical Relational Learning
Probabilistic Logic Programming
Probabilistic Programming
Fuzzy Logic
…

Sub-symbolic

Neural Symbolic Learning
Memory-based neural nets
Attention-based neural nets
Neural program synthesis
…

Hybrid Model

Recent Advances

Neural Module Networks (Andreas, et al., 2016)
Logic Tensor Network (Serafini and Garcez, 2016)
Neural Theorem Prover (Rocktäschel and Riedel, 2017)
Differential ILP (Evans and Grefenstette, 2018)
DeepProblog (Manhaeve et al., 2018)
Symbol extraction via RL (Penkov and Ramamoorthy, 2019)
Predicate Network (Shanahan et al., 2019)

Remaining Questions

Do we really need to relax logical calculi with continuous functions?
- Now we have gradients, which is good, but we also lose many other things:
  - Distributed representations vs extrapolation;
  - Probabilistic and fuzzy operators bring independent assumptions;
  - High speed inference requires pre-compiled network structures, difficult to learn first-order logical theories;
Do we really need huge amount of labelled data?
What about heavy-reasoning tasks?
How do we (humans) solve these problems?

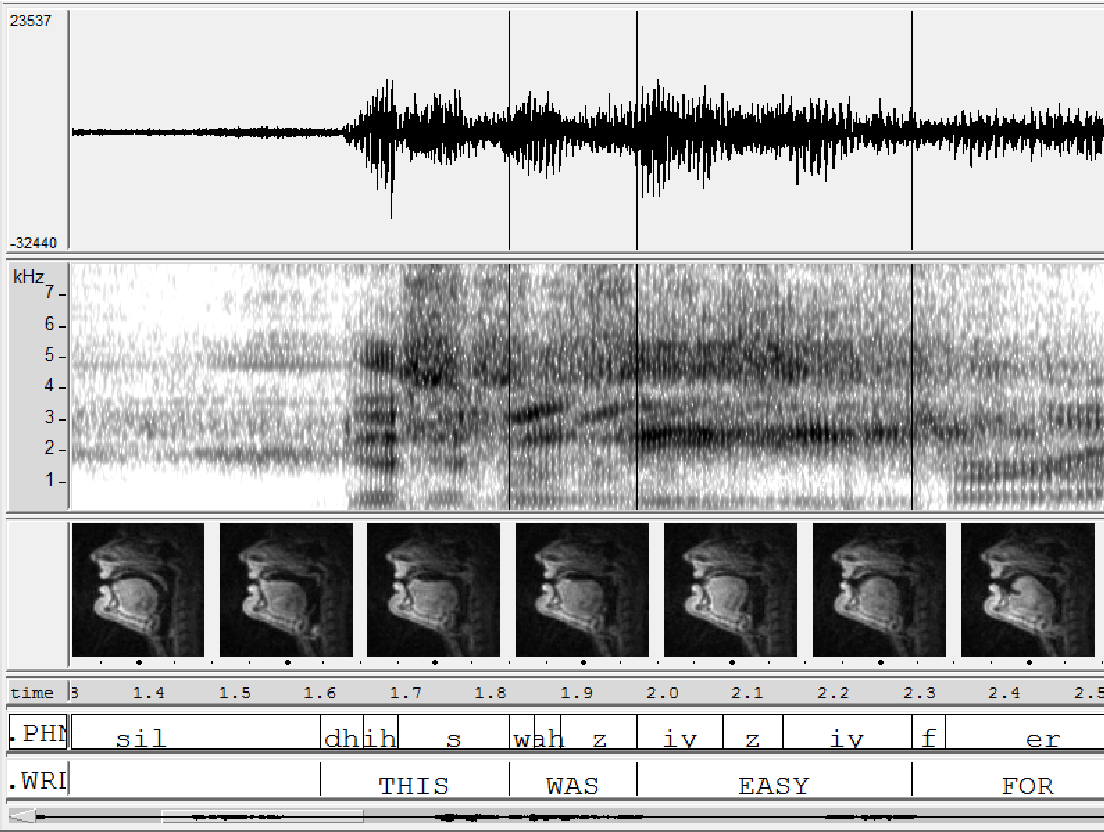
A Human Example

The Mayan Calendars

It records some big events and their dates.

The calendar

Structure

Row 1-2: $X$ (Creation)
Row 3-7: $Y$ (Long-count)
Row 8-9: $Z$ (Tzolkin & Haab)

Calculation \[ X\oplus Y=Z \]

The “head variants”

Cracking the glyphs

[Bowditch, 1901]

Cracking the glyphs

Perception:
- $\text{Glyphs}$ (image) $\mapsto$ $\text{Numbers}$ (symbol);
Abduction:
- Observation: the equations on tablet must be correct;
- Background Knowledge:
  - Calendar structure: $X\oplus Y=Z$
  - Calculation rules: 20-based $\oplus$;
- Explanation: possible digits on the tablet that are consistent with background knowledge and observation
Trial-and-errors:
- Make abductions until the perception and reasoning are consistent.

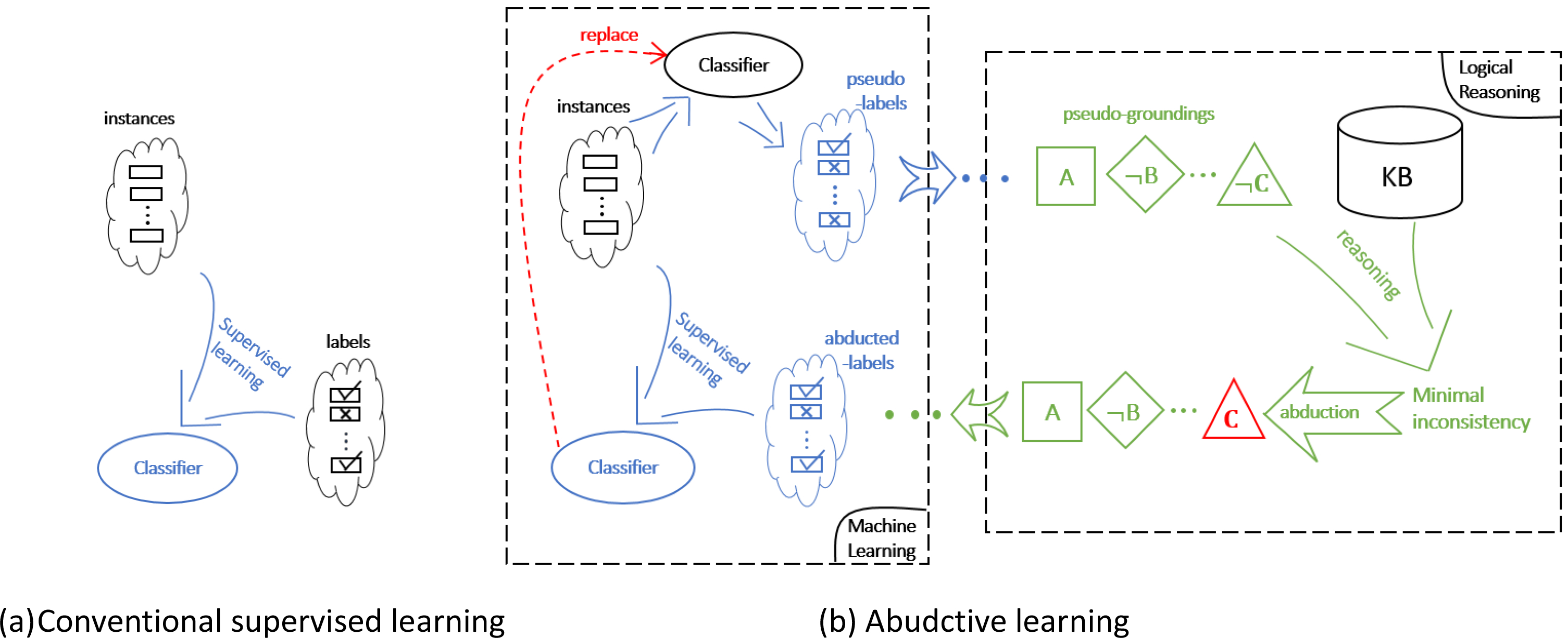
Abductive Learning

The Framework

Machine learning:
- Perception model $p$ mapping raw data ⟶ primitive logic facts;
Logical abduction:
- Abduces pseudo label (primitive logic facts facts) to re-train $p$;
- Learns logical rules $\Delta_C$ to complete the reasoning from primitive logic facts ⟶ final concept;
Optimise the consistency of hypothesis and data.

Formulation

Intuition:

Maximise the consistency between training data $D$ and hypothesis $H$:

\begin{align} \max\limits_{H=p\cup\Delta_C}\quad \text{Con}(H\cup D), \end{align}

where $\text{Con}(H\cup D)$ is the size of subset in training data that is consistent with $H$:

\begin{align} \text{Con}(H\cup D)=\max\limits_{D_c\subseteq D}\quad&\mid D_c\mid\label{eq:al:con}\\ \mathrm{s.t.}\quad&\forall \langle \mathbf{x}_i,y_i\rangle\in D_c\quad(BK\cup \Delta_C \cup p(\mathbf{x}_i)\models y_i).\nonumber \end{align}

Optimisation

Optimise the function guessing about the wrongly perceived symbols.

\begin{align} \max\limits_{\color{#CC9393}{\delta}}\quad&\text{Con}({\color{#CC9393}{\delta}}(p^t(X))\cup\Delta_C \cup D)\label{eq:al:opt2}\\ s.t.\quad&\mid\delta(p^t(X))\mid\leq M\nonumber \end{align}

Abduce consistent assignments for the wrongly perceived ones.

\begin{equation} BK\cup \Delta_C \cup {\color{#CC9393}{r}}_\delta(x) \models y \end{equation}

Compare to conventional supervised Learning

Experiments

Handwritten Equation Decipherment

Input: Image sequence only with label of equation’s correctness

Output:
- Well-trained CNN $p:\mathbb{R}^d\mapsto\{0,1,+,=\}$
- Operation rules:
  - e.g. 1+1=10, 1+0=1,…(add); 1+1=0, 0+1=1,…(xor).

Setting

Data: length 5-26 equations, each length 300 instances
- DBA: MNIST equations;
- RBA: Omniglot equations;
- Binary addition and exclusive-or.

Compared methods:
- ABL-all: Our approach with all training data
- ABL-short: Our approach with only length 7-10 equations;
- DNC: Memory-based DNN;
- Transformer: Attention-based DNN;
- BiLSTM: Seq-2-seq baseline;

Background knowledge 1

Equation structure (DCG grammars):

All equations are X+Y=Z;
Digits are lists of 0 and 1.

Background knowledge 2

Binary operation:

Calculated bit-by-bit, from the last to the first;
- Allow carries.

Implementation

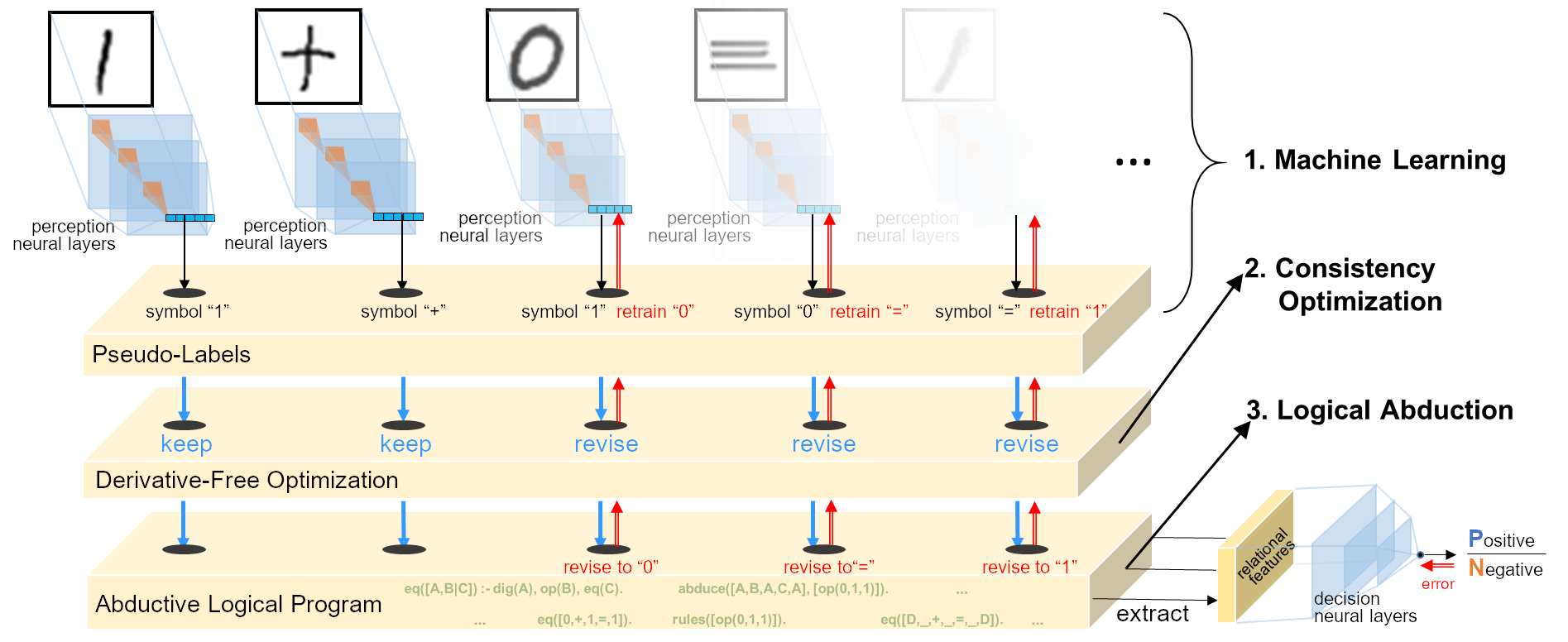
Perception model: Convolutional Neural Network
Abductive reasoning model: Abductive Logic Programming
Consistency optimisation: Derivative-Free Optimisation (RACOS)

Results

Test Acc. vs Eq. length

Training Log

%%%%%%%%%%%%%% LENGTH:  7  to  8 %%%%%%%%%%%%%%
This is the CNN's current label:
[[1, 2, 0, 1, 0, 1, 2, 0], [1, 1, 0, 1, 0, 1, 3, 3], [1, 1, 0, 1, 0, 1, 0, 3], [2, 0, 2, 1, 0, 1, 2], [1, 1, 0, 0, 0, 1, 2], [1, 0, 1, 1, 0, 1, 3, 0], [1, 1, 0, 3, 0, 1, 1], [0, 0, 2, 1, 0, 1, 1], [1, 3, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 1, 3, 3]]
****Consistent instance:
consistent examples: [6, 8, 9]
mapping: {0: '+', 1: 0, 2: '=', 3: 1}
Current model's output:
00+1+00 01+0+00 0+00+011
Abduced labels:
00+1=00 01+0=00 0+00=011
Consistent percentage: 0.3
****Learned Rules:
rules:  ['my_op([0],[0],[0,1])', 'my_op([1],[0],[0])', 'my_op([0],[1],[0])']

Train pool size is : 22

Training Log

...
This is the CNN's current label:
[[1, 1, 0, 1, 2, 1, 3, 3], [1, 3, 0, 3, 2, 1, 3], [1, 0, 1, 1, 2, 1, 3, 3], [1, 1, 0, 1, 0, 1, 3, 3], [1, 0, 1, 1, 2, 1, 3, 3], [1, 1, 0, 1, 0, 1, 3, 3], [1, 0, 3, 3, 2, 1, 1], [1, 1, 0, 1, 2, 1, 3, 3], [1, 1, 0, 1, 2, 1, 3, 3], [3, 0, 1, 1, 2, 1, 1]]
****Consistent instance:
consistent examples: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
mapping: {0: '+', 1: 0, 2: '=', 3: 1}
Current model's output:
00+0=011 01+1=01 0+00=011 00+0=011 0+00=011 00+0=011 0+01=00 00+0=011 00+0=011 1+00=00
Abduced labels:
00+0=011 01+1=01 0+00=011 00+0=011 0+00=011 00+0=011 0+01=00 00+0=011 00+0=011 1+00=00
Consistent percentage: 1.0
****Learned feature:
rules:  ['my_op([1],[0],[0])', 'my_op([0],[1],[0])', 'my_op([1],[1],[1])', 'my_op([0],[0],[0,1])']

Train pool size is : 77

Mutual Beneficial Perception & Reasoning

Training Acc.

Model Reuse

Reusing $p$ (L) vs reusing $\Delta_C$ (R)

Other classical AI techniques?

Extended visual N-queens

Constraint Logic Programming

ABL-ALP	ABL-CLP(FD)	ABL-CHR
97.6%	98.1%	97.9%

Deep Neural Net Only

CNN	Bi-LSTM
73.5%	51.3%

Conclusions

Summary

Full-featured first-order logic:
- Handles heavy-reasoning problems & has better generalisation
Requires much less labelled data on each instance of symbols;
Flexible framework with switchable parts:
- Possible to plug in many symbolic AI approaches;

Future work

Symbol invention instead of defining every primitive symbols before training;
Improve the efficiency of the trial-and-errors, because abduction in general is neither sound or complete.

Each Play to Their Strengths

: http://daiwz.net
: https://github.com/AbductiveLearning/ABL-HED