Abductive Learning
Connecting Machine Learning and Logical Reasoning
(Press ? for help, n and p for next and previous slide)
Joint work with Zhi-Hua Zhou$^*$, Stephen Muggleton$^\dagger$, Yang Yu$^*$, Qiu-Ling Xu$^*$ Yu-Xuan Huang$^*$ and Le-Wen Cai$^*$.
$^\dagger$Department of Computing, Imperial College London
$^*$Department of Computer Science, Nanjing University
Motivation
Data-Driven AI
Adding data to improve the model:
A Modern Rephrase of Curve Fitting
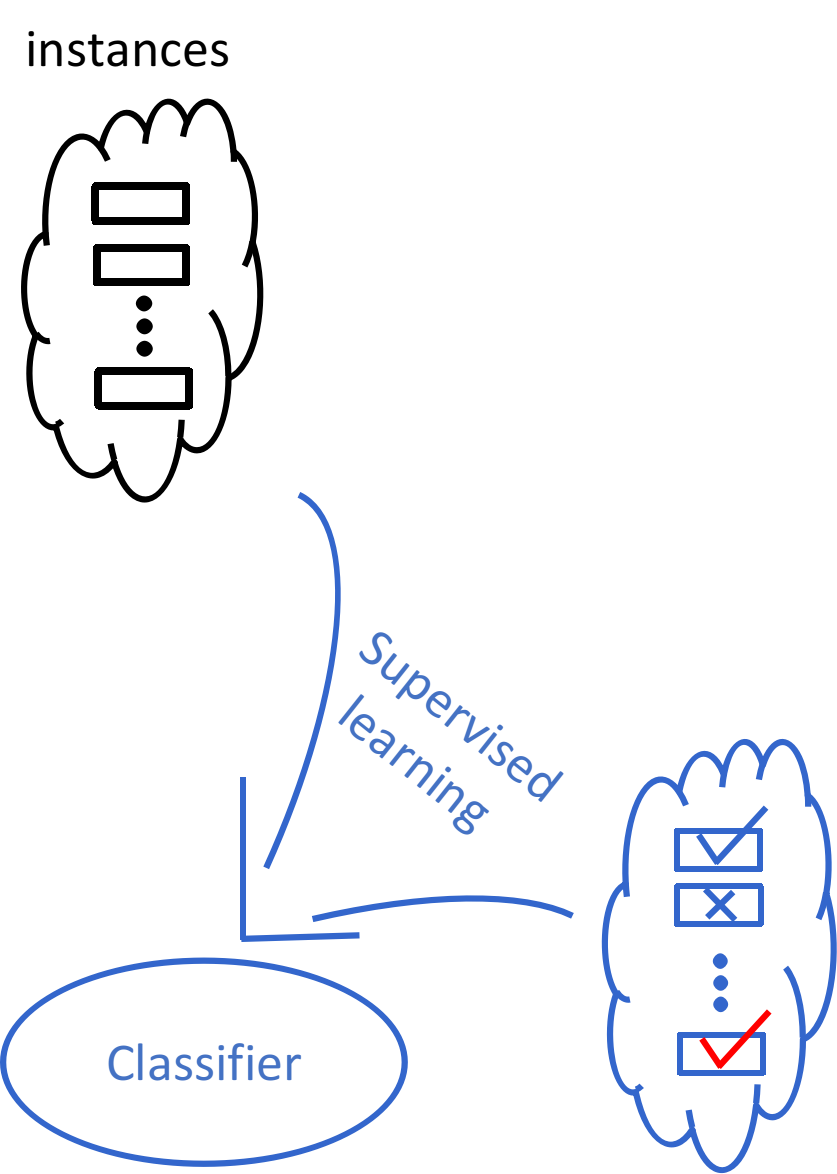
 Supervised Learning
Supervised Learning
Heavy Learning / Light Reasoning
Data (alone) could be never enough…
Human: How many eyes does a giraffe have?
GPT-3: A giraffe has two eyes.
Human: How many eyes does my foot have?
GPT-3: Your foot has two eyes.
Human: How many eyes does a spider have?
GPT-3: A spider has eight eyes.
Human: How many eyes does the sun have?
GPT-3: The sun has one eye.
Human: How many eyes does a blade of grass have?
GPT-3: A blade of grass has one eye.
Knowledge-Driven AI
e.g., Logic Programs:
- Use logic clauses to represent knowledge;
- Use logical inference to manipulate it;
- A declarative programming language with theoretical guarantee.

Knowledge-Driven AI
Adding knowledge to speed-up problem solving and learning:
- Theorem provers
- Rule-based expert systems
- Intelligent forms of search (semantic web, knowledge graph, etc.)
- Constraint-based approaches (SAT, CLP, SMT, etc.)
- Program synthesis / Inductive Logic Programming
Example: Learning Quick Sort
Examples:
Background Knowledge (Primitive Predicates):
Leanred Hypothesis:
Heavy Reasoning / Light Learning
Cannot solve problems like this…
Combining The Two Systems
Yoshua Bengio: From System 1 Deep Learning to System 2 Deep Learning.
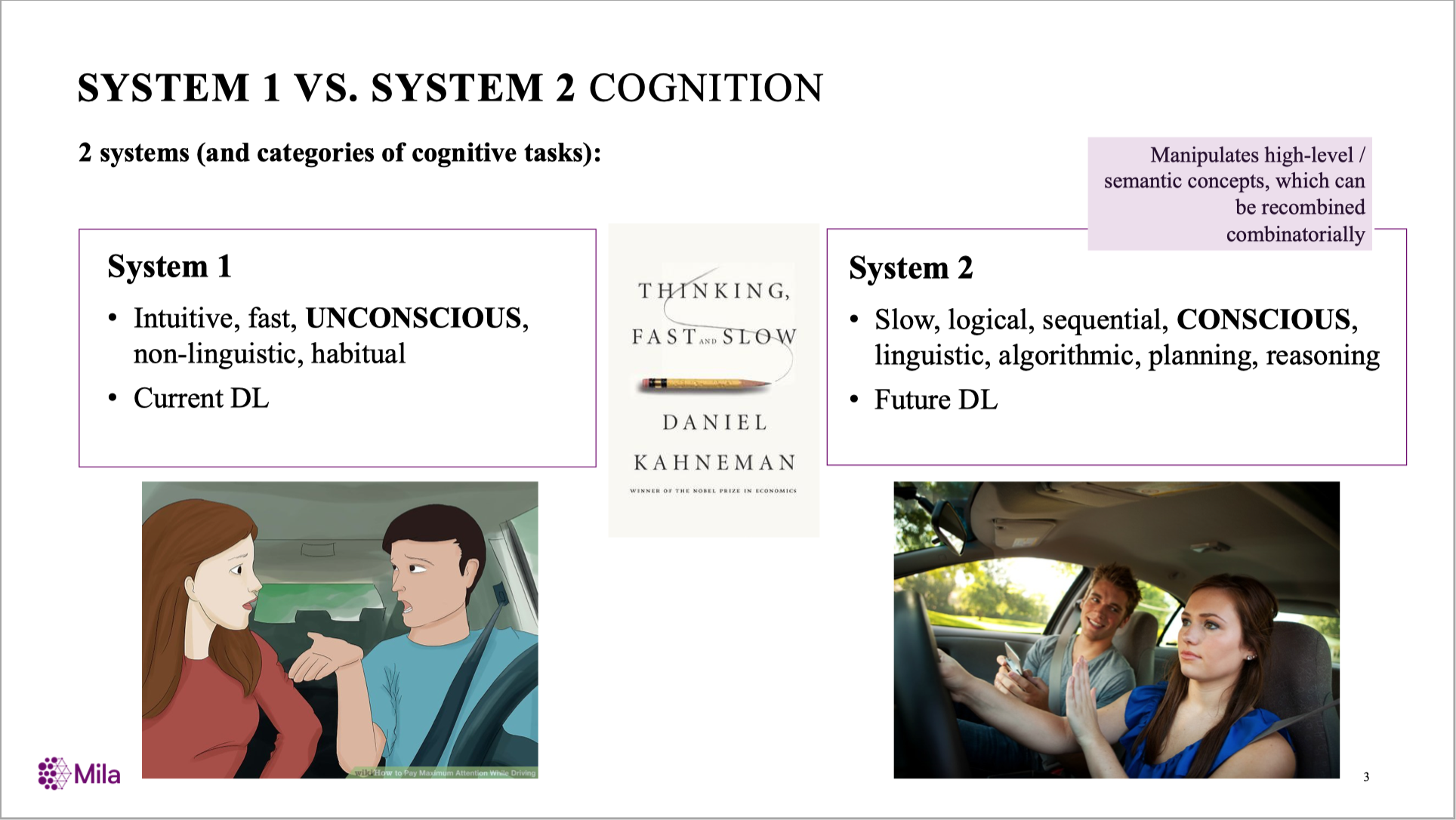
(NeurIPS’2019 Keynote)
Recently: Neuro-Symbolic Learning
- Neural Module Networks (Andreas, et al., 2016)
- Logic Tensor Network (Serafini and Garcez, 2016)
- Neural Theorem Prover (Rocktäschel and Riedel, 2017)
- Differential ILP (Evans and Grefenstette, 2018)
- DeepProblog (Manhaeve et al., 2018)
- Symbol extraction via RL (Penkov and Ramamoorthy, 2019)
- Predicate Network (Shanahan et al., 2019)
Neural Theorem Prover (Rocktäschel and Riedel, 2017)
Heavy Learning / Light Reasoning
Difficult to extrapolate:
(Trask et al., 2018)
How About Pure Symbolic Knowledge?
| Representation | Statistical / Neural | Symbolic |
|---|---|---|
| Examples | Many | Few |
| Data | Tables | Programs / Logic programs |
| Hypotheses | Propositional/functions | First/higher-order relations |
| Explainability | Difficult | Possible |
| Knowledge transfer | Difficult | Easy |
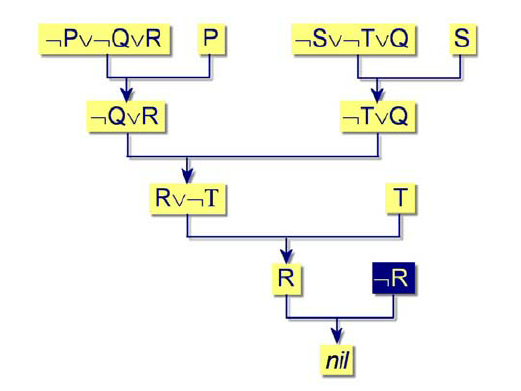
Abductive Reasoning:
A Human Example
The “head variants”

Mayan Calendar
Cracking the glyphs: They Must Be Consistent!
- (1.18.5.4.0): the 275480 day from origin
- (1 Ahau): the 40th day of that year
- (13 Mac): in the 13 month of that year
Abductive Reasoning
The Abductive Learning Framework
The Framework
Training examples: $⟨ x,y⟩ $.
- Machine learning (e.g., neural net):
\[ z=f(x;\theta)=\text{Sigmoid}(P_\theta(z|x))\]
- Learns a perception model mapping raw data (\(x\)) ⟶ logic facts (z);
- Logical Reasoning (e.g., logic program):
\[B\cup z\models y\]
- Deduction: infers the final output (\(y\)) based on \(z\) and background knowledge (\(B\));
- Abduction: infers pseudo label (revised facts) $z'$ to improve perception model $f(x;\theta)$;
- Induction: learns (first-order) logical theory \(H\) such that \(B\cup \color{#CC9393}{H}\cup z\models y\);
- Optimisation:
- Maximises the consistency of \(H\cup z\) and \(f\) w.r.t. \(\langle x, y\rangle\) and \(B\).
Supervised Learning
Abductive Learning (ABL)
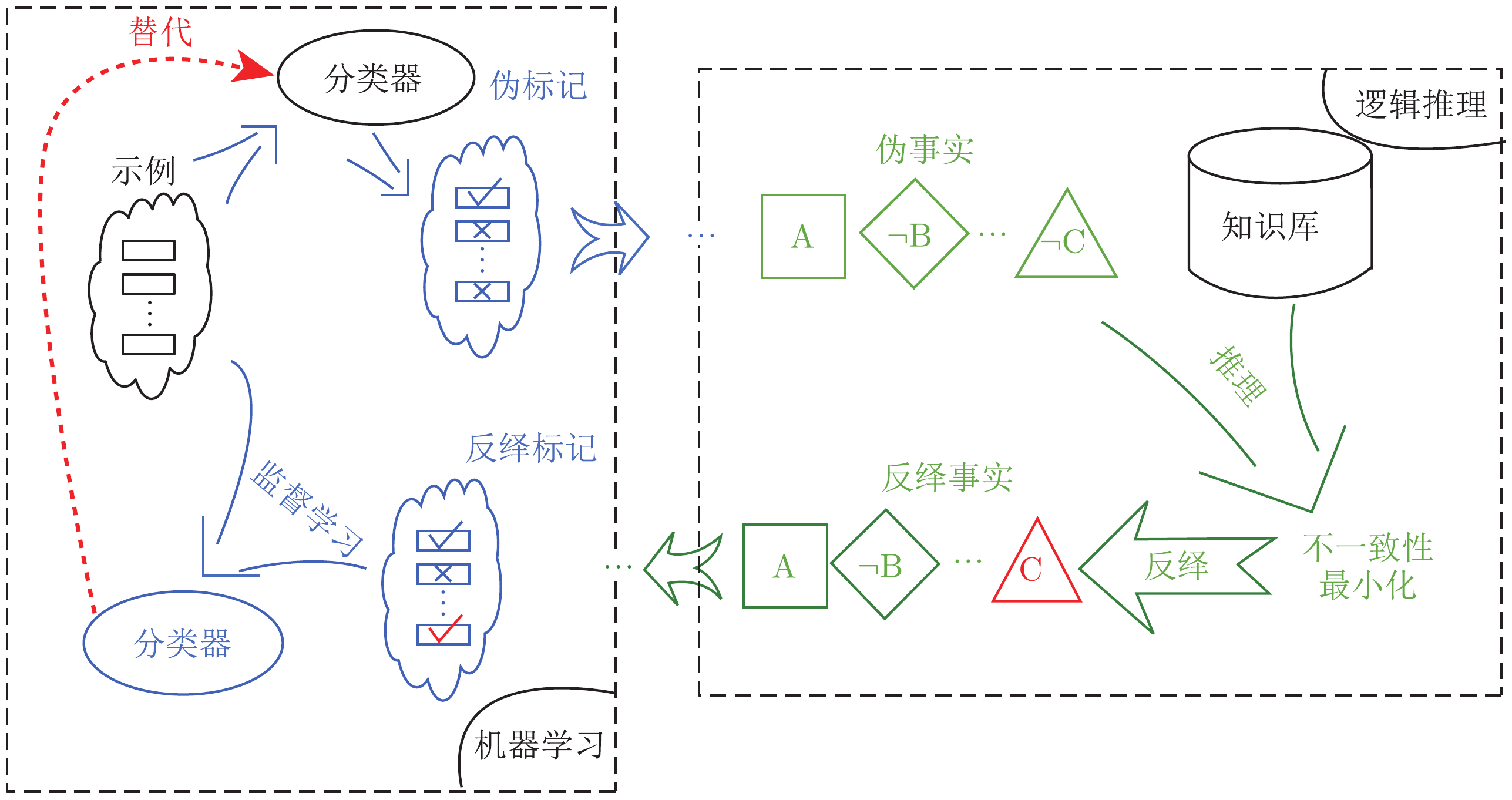
A Flexible Framework
ABL is a framework where machine learning and logical reasoning can be entangled and mutually beneficial.
- Machine Learning: Utilising labelled data / pre-trained model;
- Optimisation: Measuring consistency in different ways;
- Logical Reasoning: Refining incomplete background knowledge / learning logical rules;
Abduction By
Heuristic Search
Handwritten Equation Decipherment
Task: Image sequence only with label of equation’s correctness
- Untrained image classifier (CNN) \(f:\mathbb{R}^d\mapsto\{0,1,+,=\}\)
- Unknown rules: e.g.
1+1=10,1+0=1,…(add);1+1=0,0+1=1,…(xor). - Learn perception and reasoning jointly.
Background knowledge 1
Equation structure (DCG grammars):

- All equations are
X+Y=Z; - Digits are lists of
0and1.
Background knowledge 2
Binary operation:

- Calculated bit-by-bit, from the last to the first;
- Allow carries.
Implementation
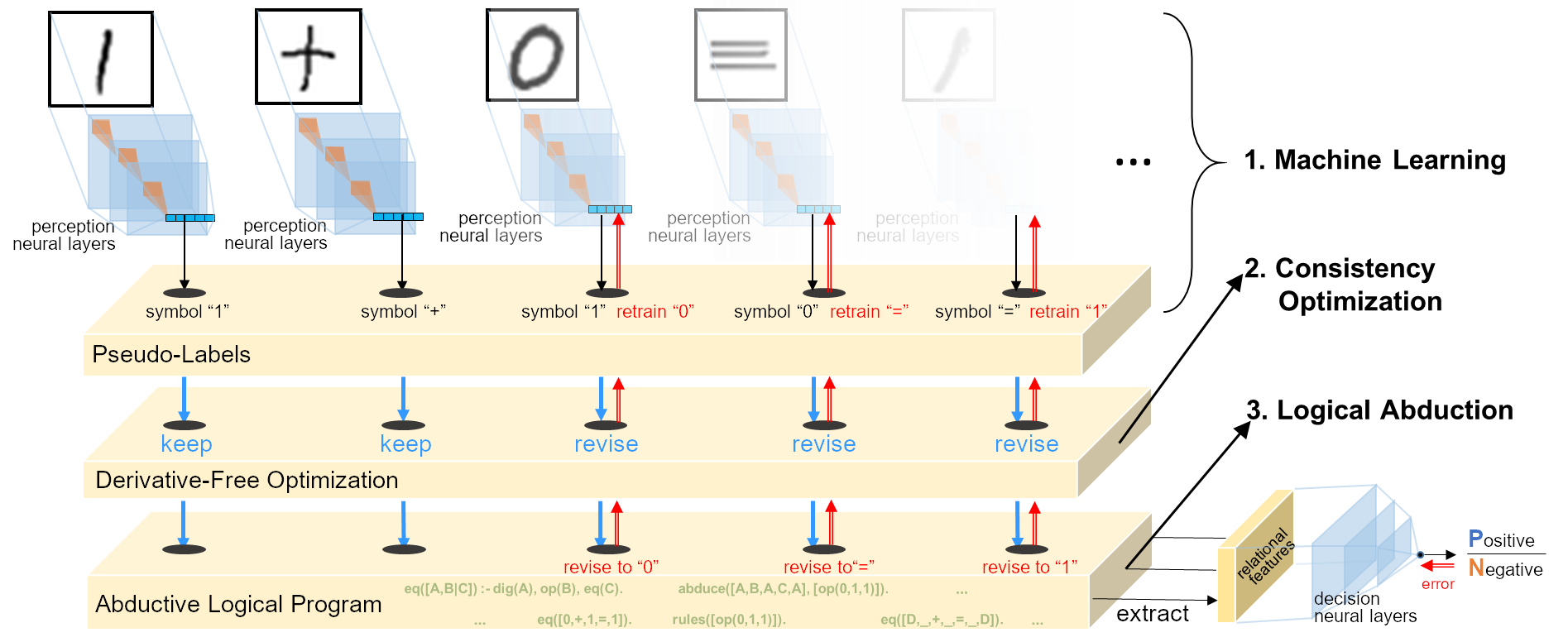
Optimise consistency by Heuristic Search
- Heuristic function for guessing the wrongly perceived symbols: \[\text{symbols to be revised}=\delta(z)\]
- Abduce revised assignments of \(\delta(z)\) that guarantee consistency: \[ B\cup H\cup \underbrace{\overbrace{z\backslash\delta(z)}^{\text{unchange}} \cup \overbrace{{\color{#CC9393}{r_\delta}}(z)}^{\text{revise}}}_{\text{pseudo-labels }z'} \models y \]
Experiment
- Data: length 5-26 equations, each length 300 instances
- DBA: MNIST equations;
- RBA: Omniglot equations;
- Binary addition and exclusive-or.
- Compared methods:
- ABL-all: Our approach with all training data
- ABL-short: Our approach with only length 7-10 equations;
- DNC: Memory-based DNN;
- Transformer: Attention-based DNN;
- BiLSTM: Seq-2-seq baseline;
Training Log
%%%%%%%%%%%%%% LENGTH: 7 to 8 %%%%%%%%%%%%%%
This is the CNN's current label:
[[1, 2, 0, 1, 0, 1, 2, 0], [1, 1, 0, 1, 0, 1, 3, 3], [1, 1, 0, 1, 0, 1, 0, 3], [2, 0, 2, 1, 0, 1, 2], [1, 1, 0, 0, 0, 1, 2], [1, 0, 1, 1, 0, 1, 3, 0], [1, 1, 0, 3, 0, 1, 1], [0, 0, 2, 1, 0, 1, 1], [1, 3, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 1, 3, 3]]
****Consistent instance:
consistent examples: [6, 8, 9]
mapping: {0: '+', 1: 0, 2: '=', 3: 1}
Current model's output:
00+1+00 01+0+00 0+00+011
Abduced labels:
00+1=00 01+0=00 0+00=011
Consistent percentage: 0.3
****Learned Rules:
rules: ['my_op([0],[0],[0,1])', 'my_op([1],[0],[0])', 'my_op([0],[1],[0])']
Train pool size is : 22
...
This is the CNN's current label:
[[1, 1, 0, 1, 2, 1, 3, 3], [1, 3, 0, 3, 2, 1, 3], [1, 0, 1, 1, 2, 1, 3, 3], [1, 1, 0, 1, 0, 1, 3, 3], [1, 0, 1, 1, 2, 1, 3, 3], [1, 1, 0, 1, 0, 1, 3, 3], [1, 0, 3, 3, 2, 1, 1], [1, 1, 0, 1, 2, 1, 3, 3], [1, 1, 0, 1, 2, 1, 3, 3], [3, 0, 1, 1, 2, 1, 1]]
****Consistent instance:
consistent examples: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
mapping: {0: '+', 1: 0, 2: '=', 3: 1}
Current model's output:
00+0=011 01+1=01 0+00=011 00+0=011 0+00=011 00+0=011 0+01=00 00+0=011 00+0=011 1+00=00
Abduced labels:
00+0=011 01+1=01 0+00=011 00+0=011 0+00=011 00+0=011 0+01=00 00+0=011 00+0=011 1+00=00
Consistent percentage: 1.0
****Learned feature:
Rules: ['my_op([1],[0],[0])', 'my_op([0],[1],[0])', 'my_op([1],[1],[1])', 'my_op([0],[0],[0,1])']
Train pool size is : 77
Performance
Test Acc. vs Eq. length
Semi-Supervised
Abductive Learning
Theft Judicial Sentencing
Task: predict punishment from court record (text).
- 687 court records in Guizhou, China;
- Sentence-level tagging by experts;
- Domain Knowledge: Laws;
- Target: Using knowledge and unlabelled data to reduce the labelling cost.
Model Overview
- Each document (court record of theft) is associated with the amount of stolen money, which is used for calculating the benchmark punishment;
- BERT is used to extract the sentencing elements;
- Regression model predicts the final sentence according to the benchmark and extracted elements.
Abduction by Regression
Experiments
- Supervised:
- BERT (Devlin et al., 2018);
- ABL;
- Semi-supervised
- Pseudo-labeling (Lee, 2013);
- Tri-training (Zhou and Li, 2005);
- SS-ABL;
Results
| Method | F1 |
|---|---|
| BERT-10 | 0.811±0.010 |
| PL-10 | 0.814±0.006 |
| Tri-10 | 0.812±0.016 |
| ABL-10 | 0.824±0.014 |
| SS-ABL-10 | 0.862±0.005 |
| BERT-50 | 0.857±0.006 |
| PL-50 | 0.858±0.010 |
| Tri-50 | 0.861±0.007 |
| ABL-50 | 0.860±0.003 |
| SS-ABL-50 | 0.865±0.007 |
| BERT-100 | 0.863±0.003 |
| ABL-100 | 0.867±0.008 |
| Method | MAE | MSE |
|---|---|---|
| BERT-10 | 0.8668±0.0320 | 1.2044±0.1233 |
| PL-10 | 0.8616±0.0346 | 1.1548±0.1073 |
| Tri-10 | 0.8402±0.0659 | 1.1548±0.1073 |
| ABL-10 | 0.8728±0.1016 | 1.3756±0.2168 |
| SS-ABL-10 | 0.8239±0.0174 | 1.1459±0.0487 |
| BERT-50 | 0.8300±0.0198 | 1.0654±0.0443 |
| PL-50 | 0.8316±0.0346 | 1.0448±0.1543 |
| Tri-50 | 0.8102±0.0213 | 0.9944±0.0461 |
| ABL-50 | 0.8416±0.0294 | 1.0821±0.1097 |
| SS-ABL-50 | 0.7876±0.0272 | 0.9591±0.0910 |
| BERT-100 | 0.8213±0.0141 | 1.0114±0.0312 |
| ABL-100 | 0.8223±0.0302 | 1.0065±0.0931 |
Abductive Knowledge Induction
Example: Accumulative Sum
A task from Neural arithmetic logic units (Trask et al., NeurIPS 2018).
- Examples: Sequences of handwritten digit images (\(x\)) with their sums (\(y\));
- Task:
- Perception: An image recognition model \(f: \text{Image}\mapsto \{0,1,\ldots,9\}\); \[z=f(x)=f([img_1, img_2, img_3])=[7,3,5]\]
- Reasoning: A program to calculate the output \(y\).
:- Z = [7,3,5], Y = 15, prog(Z, Y).
% true.
A Probabilistic Model
\[ \underset{\theta}{\operatorname{arg max}}\sum_z \sum_H P(y,z,H|B,x,\theta) \]
- \(\theta\): parameter of machine learning model;
- \(z\): unknown pseudo-labels;
- \(H\): missing logic rules.
EM-based Learning
- Expectation: Estimate the expectation of the symbolic hidden variables;
\[\hat{H}\cup\hat{z}=\mathbb{E}_{(H,z)\sim P(H,z|B,x,y,\theta)} [H\cup z]\]
- Calculate the expectation by sampling: \(P(H,z|B,x,y,\theta)\propto P(y,H,z|B,x,\theta)\) \[P(y,H,z|B,x,\theta)=\underbrace{P(y|B,H,z)}_{\text{logical abduction}} \cdot \overbrace{P_{\sigma^*}(H|B)}^{\text{Prior of program}} \cdot \underbrace{P(z|x,\theta)}_{\text{Prob. of Poss. Wrld.}}\]
- Maximisation: Optimise the neural parameters to maximise the likelihood. \[\hat{\theta}=\underset{\theta}{\operatorname{arg max}}P(Z=\hat{z}|x,\theta)\]
Example: Abduction-Induction Learning
#=is a CLP(Z) predicate for representing arithmetic constraints:- e.g.,
X+Y#=3, [X,Y] ins 0..9will outputX=0, Y=3; X=1, Y=2; ...
- e.g.,
Experiments
- Tasks: MNIST calculations
- Accumulative sum/product;
- Bogosort (permutation sort);
- Compared methods and domain knowledge:
| Domain Knowledge | End-to-end Models | \(Meta_{Abd}\) |
|---|---|---|
| Recurrence | LSTM & RNN | Prolog’s list operations |
| Arithmetic functions | NAC & NALU (Trask et al., 2018) |
Predicates add, mult and eq |
| Permutation | Permutation matrix \(P_{sort}\) (Grover et al., 2019) | Prolog’s permutation |
| Sorting | sort operator (Grover et al., 2019) |
Predicate s (learned as sub-task) |
Accumulative Sum/Product
Learned Programs:
%% Accumulative Sum
f(A,B):-add(A,C), f(C,B).
f(A,B):-eq(A,B).
%% Accumulative Product
f(A,B):-mult(A,C), f(C,B).
f(A,B):-eq(A,B).
Bogosort
Learned Programs:
% Sub-task: Sorted
s(A):-s_1(A,B),s(B).
s(A):-tail(A,B),empty(B).
s_1(A,B):-nn_pred(A),tail(A,B).
%% Bogosort by reusing s/1
f(A,B):-permute(A,B,C),s(C).
- The subtask
sorted/1uses the subset of sorted MNIST sequences in training data as example.
Program Induction: Abductive vs Non-Abductive
- \(z\rightarrow H\): Sample \(z\) according to \(P_\theta(z|x)\) and then call conventional MIL to learn a consistent \(H\);
- \(H\rightarrow z\): Combining abduction with induction using \(Meta_{abd}\).
Conclusion
Conclusions
- Full-featured logic programs:
- Exploits symbolic domain knowledge
- Learns recursive programs and invents predicates
- Better extrapolation
- Requires much less training data
- Flexible framework with switchable parts:
- Improving the optimisation efficiency;
- New symbol discovery instead of defining every primitive symbols before training;
- More applications on real data;
Thanks!
References:
- W.-Z. Dai, S. H. Muggleton. Abductive Knowledge Induction From Raw Data, arXiv, 2010.03514, 2020.
- Y.-X. Huang, W.-Z. Dai, J. Yang, L.-W. Cai, S. Cheng, R. Huang, Y.-F. Li and Z.-H. Zhou, Semi-Supervised Abductive Learning and Its Application to Theft Judicial Sentencing, In: Proceedings of 20th IEEE International Conference on Data Mining (ICDM’20). Sorrento, Italy, 2020.
- W.-Z. Dai, Q.-L. Xu, Y. Yu, and Z.-H. Zhou. Bridging machine learning and logical reasoning by abductive learning. In: Advances in Neural Information Processing Systems 32 (NeurIPS’19). Vancouver, Canada, 2019.
- Z.-H. Zhou. Abductive learning: Towards bridging machine learning and logical reasoning. Science China Information Sciences, 2019, vol.62, 076101.


