符号学习简介
神经符号学习
(Press ? for help, n and p for next and previous slide)
路径图
符号学习
神经符号学习
https://daiwz.net
神经符号学习
- KBMC
- Embedding 与命题化
- 特殊神经模块
- 混合模型
符号学习
神经符号学习
https://daiwz.net
另一种 KBMC
Knowledge-Based Model Construction where \(model=NN\):构建具有逻辑结构的神经网络模型
符号学习
神经符号学习
https://daiwz.net
KBANN
Knowledge-Based Artificial Neural Networks [Towell & Shavlik, 1994]
动机:两种 AI 实现方式的结合
- 专家系统(Hand-built classifiers):
- 知识的完备性与可靠性难以保证
- 背景知识过于复杂,导致推理非常困难(intractable)
- 人工编写的知识难以改变
- 机器学习(Empirical learning):
- 特征选择对模型性能影响过大
- 不同任务需要使用不同的特征
- 特征构建(在原始特征基础上生成新特征)风险高
- 仅仅关注统计意义上的“大部分”,泛化时容易忽略 outliers
符号学习
神经符号学习
https://daiwz.net
KBANN
连接和权重的设置:
- 将逻辑表达式转化为一个 MLP
- body literals 对公式的影响相同,因此只有一个权重
符号学习
神经符号学习
https://daiwz.net
KBANN
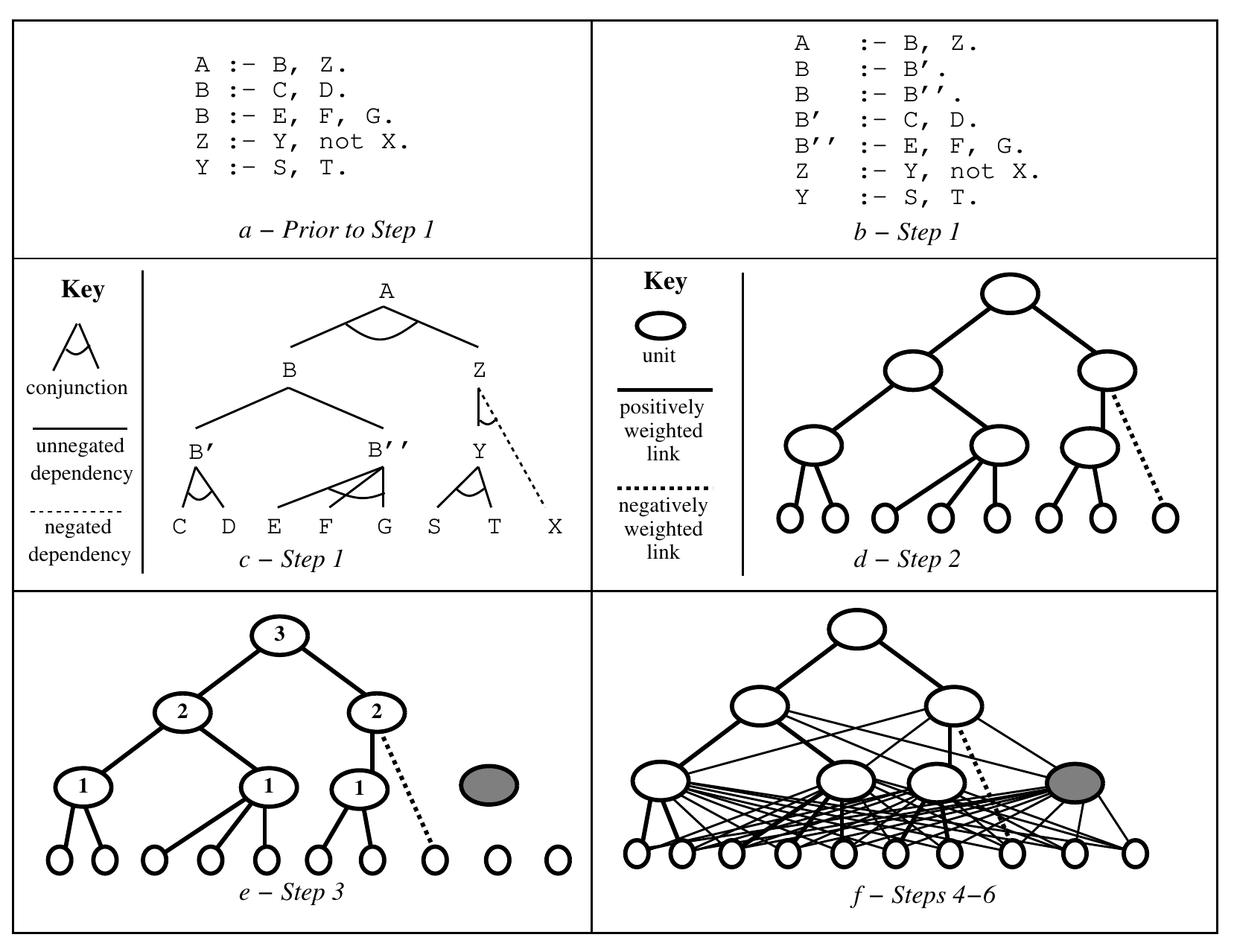
转换析取式,例如:
\begin{eqnarray*} A& \leftarrow& B, C, D.\\ A& \leftarrow& D, E, F, G. \end{eqnarray*}转换为:
\begin{eqnarray*} A&\leftarrow& A'\\ A'& \leftarrow& B, C, D.\\ A&\leftarrow& A''\\ A''& \leftarrow& D, E, F, G. \end{eqnarray*}- 将规则转换为神经网络
- 添加隐层节点(可选)
- 添加神经元连接
符号学习
神经符号学习
https://daiwz.net
逻辑程序并行计算模型
Parallel Computational Model for Logic Programming [Hölldobler & Kalinke, 1994]
- 非定子句(definite clause)构成的逻辑理论 \(P\) 对于 immediate consequence 算子 \(T_P\) 可能不存在不动点,其语义无法定义。
- 将 \(T_P\) 算子延拓为一个完备测度空间(如 Banach 空间)上的映射,即可保证它存在不动点。
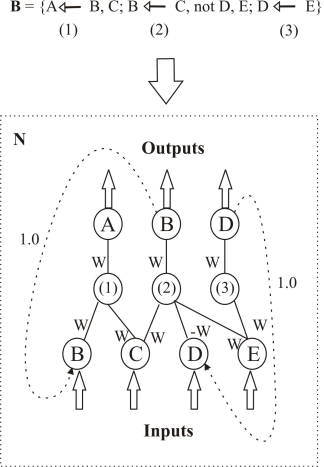
做法:将 \(T_P\) 算子表示为一个 RNN
- 与 KBANN 类似,命题原子表示神经元;
- 区别在于,每个公式是一个隐层节点;
例子:\(\{A\leftarrow B;A\leftarrow C\wedge D;A\leftarrow E\wedge F\}\)
- 节点内的数值为激活权重;
符号学习
神经符号学习
https://daiwz.net
CI\(^2\)LP
The Connectionist Inductive Learning and Logic Programming System [d’A. Garcez & Zaverucha, 1999]
- 定义两种激活阈值:
- \(0< A_{\text{min}}< 1\):当神经元取值 \(A\geq A_{\text{min}}\) 时输出 \(true\);
- \(-1 < A_{\text{max}}< 0\):当神经元取值 \(A\leq A_{\text{max}}\) 时输出 \(false\);
- 逻辑子句(长度 \(k_l\))隐层神经元激活阈值 \(\theta_l\) : \[\theta_l=\frac{(1+A_{\text{min}})(k_l-1)}{2}W\]
- 逻辑命题(定子句数 \(\mu_l\))神经元激活阈值 \(\theta_A\) : \[\theta_A=\frac{(1+A_{\text{min}})(1-\mu_l)}{2}W\]
- 隐层采用 sigmoid 激活函数,命题原子采用线性激活函数。
符号学习
神经符号学习
https://daiwz.net
CILP++
CILP with Bottom Clause Propositionalization [França, et. al., 2014]
将 CI\(^2\)LP 改进为一阶模型:
- 利用 Progol 的
mode语言定义背景知识; - 通过逆蕴涵或其他方式构建底子句(bottom clauses)
- 将底子句中的原子与子句分别作为神经元与隐层节点,用类似 CI\(^2\)LP 的方式构建神经网络;
- 将所有样本命题化为向量,并进行学习。
符号学习
神经符号学习
https://daiwz.net
神经网络中的符号规则抽取
与 KBMC 神经网络类似,一般神经网络同样可以抽取命题逻辑规则:
- Survey and critique of techniques for extracting rules from trained neural networks [Andrews, Diederich & Tickle, 1995]
- Symbolic knowledge extraction from trained neural networks: A sound approach [dA’. Garcez, Broda & Gabbay, 2001]
- Extracting Symbolic Rules from Trained Neural Network Ensembles [Zhou, Jiang & Chen, 2003]
符号学习
神经符号学习
https://daiwz.net
神经符号学习
- KBMC
- Embedding 与命题化
- 特殊神经模块
- 混合模型
符号学习
神经符号学习
https://daiwz.net
基于嵌入式表示的方法
基本思想:
- 基本放弃符号表示,将符号表示在 embedding space
- 仅仅采用 embedding space 中的向量(张量)运算来推理
- 利用 Fuzzy operators 来近似逻辑演算
符号学习
神经符号学习
https://daiwz.net
Neural Tensor Network
Reasoning with neural tensor networks for knowledge base completion [Socher et. al., 2013]
被应用在知识图谱的关系补全中:
符号学习
神经符号学习
https://daiwz.net
NTN 的训练
其中,
- \(v_{e_i}\in\mathbb{R}^d\) 实体 \(e_i\) 的 embedding
- \(h=v_{e_1}^TW_r^{[1:k]}v_{e_2}\) 将三元组 embedding 通过双线性(bilinear)映射成一个向量
- \(W_r^{[1:k]}\in\mathbb{R}^{d\times d\times k}\) 关系 \(r\) 的embedding
- \(u_r\in\mathbb{R}^k\) 、 \(M_r\in\mathbb{R}^{k\times 2d}\) 和 \(b_r\in\mathbb{R}^k\) 均为神经网络中与 \(r\) 相关的参数 \(\Theta_r\)
符号学习
神经符号学习
https://daiwz.net
Logic Tensor Network
LTN [Badreddine, et. al., 2022] 试图将 NTN 扩展为更完整的 FOL 语言。
公式 \(\phi\) 的真值用函数 \(\mathcal{G}(\phi; \Theta)\) 表示,其中
- Grounding \(p(e_1, \ldots, e_k)\) 的计算方式与 NTN 类似:
\[\mathcal{G}(p(e_1, \ldots, e_k))=\mathbf{v}W_p \mathbf{v}^T\]
- \(W_p\) 为谓词 \(p/k\) 的 embedding
- \(\mathbf{v}=(v_{e_1}, \ldots, v_{e_k})\) 是 \(k\) 个 embedding 向量的拼接
符号学习
神经符号学习
https://daiwz.net
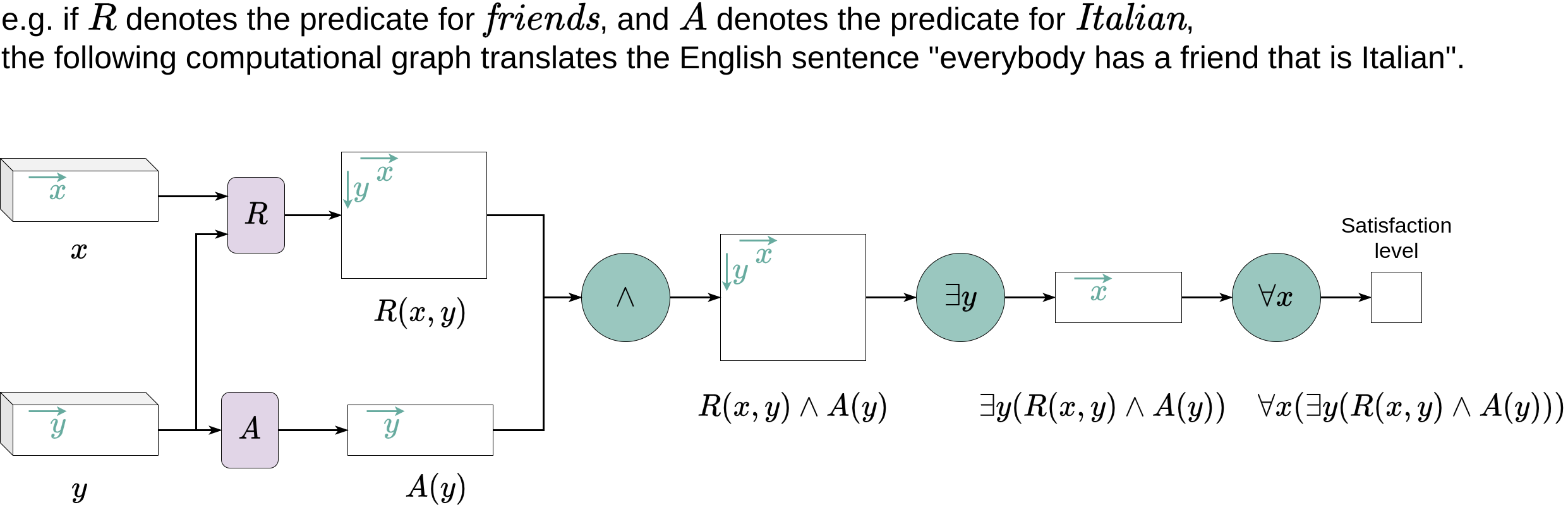
Logic Tensor Network
LTN [Badreddine et. al., 2022] 试图将 NTN 扩展为更完整的 FOL 语言。
- 对于含有逻辑连词的公式,用 fuzzy operators 来近似其推理模式
符号学习
神经符号学习
https://daiwz.net
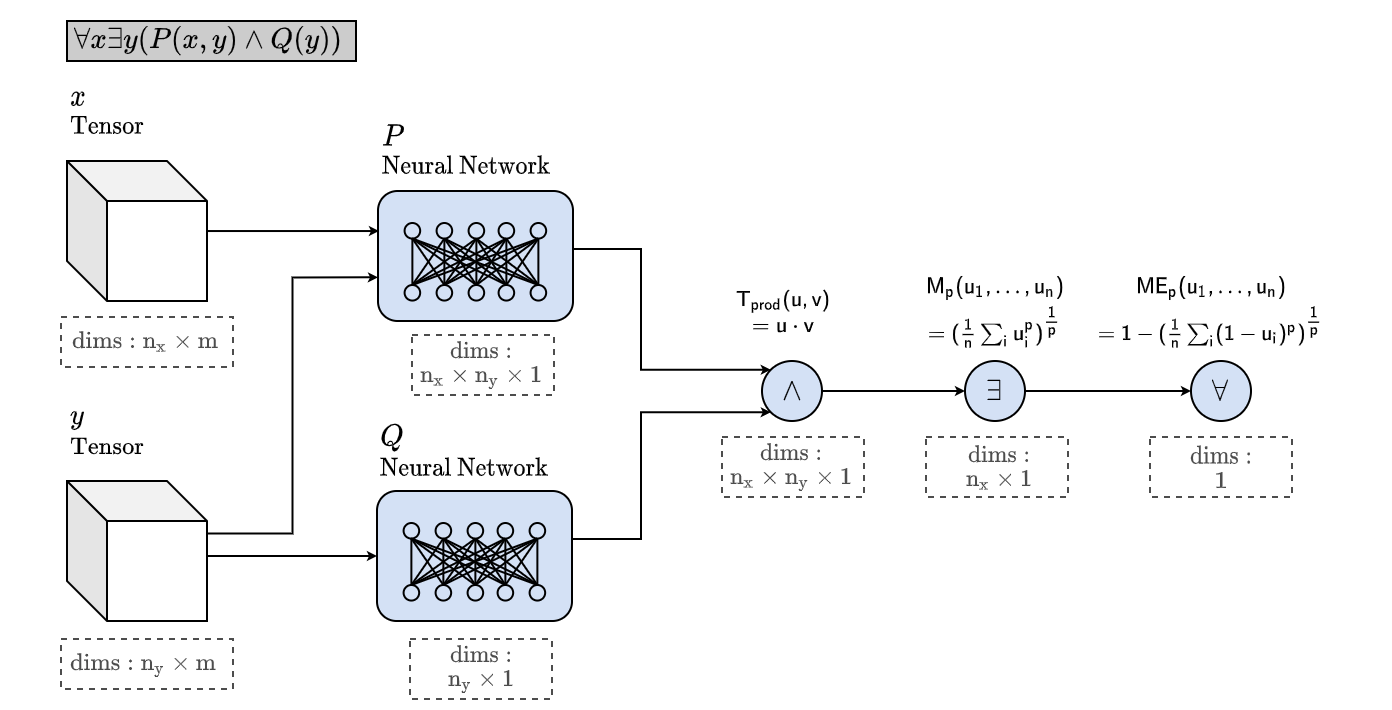
Logic Tensor Network
LTN [Badreddine et. al., 2022] 试图将 NTN 扩展为更完整的 FOL 语言。
一阶演算的实现方式:将常量的 embeddings 拼接成矩阵
符号学习
神经符号学习
https://daiwz.net
Logic Tensor Network
LTN [Badreddine et. al., 2022] 试图将 NTN 扩展为更完整的 FOL 语言。
符号学习
神经符号学习
https://daiwz.net
Neural Theorem Prover
NTP[Rocktäschel et. al., 2015] 试图模仿 SLD-Resolution(称为 backward chaining)实现推理。
- 与 KBANN 类似,用逻辑规则初始化(编译)网络结构
- 用 metarule 初始化则可达到归纳和谓词发明的效果
- 需要定义最大递归深度 \(d\)
- 用 metarule 初始化则可达到归纳和谓词发明的效果
- 用神经网络 \(\mathtt{unify}_\theta(A,B,S)=S'\) 实现合一操作
- \(A\) 与 \(B\) 为待合一的两个原子公式(embedding 拼接向量)
- \(S\) 与 \(S'\) 分别为合一进行之前/之后的证明状态
- 包含合一操作中使用的替换、成功概率等等
- 用神经网络 \(\mathtt{AND}\) 与 \(\mathtt{OR}\) 实现和取和析取
符号学习
神经符号学习
https://daiwz.net
命题化 vs Embeddings
Propositionalization and Embeddings: Two Sides of the Same Coin [Lavrac et. al., 2020]
- 命题化:用关系型特征将知识库转化为表格数据(one-hot)
- 每个维度代表一个符号
- Embedding:将符号表示在一个连续度量空间中
- 符号表示分散在不同维度中
符号学习
神经符号学习
https://daiwz.net
TensorLog
TensorLog: A Differentiable Deductive Database [Cohen, 2016]
为了解决 embedding 的泛化性问题:
- 常量 \(c_i\in\mathcal{C}\) 表示为 one-hot 向量 \(\mathbf{u}_c\)
- 二元谓词 \(r\) 则用一个稀疏矩阵 \(\mathbf{M}_r\) 表示
- \(\mathbf{M}_r^{i,j}=1\) 当且仅当 \(r(c_i, c_j)=true\)
- 一元谓词退化为一个向量 \(\mathbf{v}_r\)
- 原子公式 \(x=r(a,b)\) 的赋值 \[\mathbf{v}_a^T\mathbf{M}_r\mathbf{v}_b\]
符号学习
神经符号学习
https://daiwz.net
TensorLog
TensorLog: A Differentiable Deductive Database [Cohen, 2016]
- 可以对带权的链式规则进行推理 \[\]
- 求解 \(r(Y,X)\leftarrow s(Y,Z)\wedge t(Z,Y)\) 当 \(X=x\) 时 \(r(Y,x)\) 对哪些 \(Y\) 成立 \[\mathbf{s}(x)=\mathbf{M}_{s}\cdot\mathbf{M}_{t}\cdot\mathbf{v}_x\]
- 求解上式对某个 \(Y=y\) 是否成立 \[\text{score}(y|x)=\mathbf{v}_y^T\cdot\mathbf{s}(x)\]
符号学习
神经符号学习
https://daiwz.net
\(\partial\)ILP
\(\partial\)ILP [Evans & Grefenstette, 2018] 更进一步地将元解释学习(MIL)的方式表示为可微分计算
- 利用 \(H^2_2\) meta-rule 将所有可能的候选模型构建出来
- 用 one-hot 向量表达空间状态
- 用神经网络来近似 immediate consequence 算子
- 用 fuzzy operators 进行逻辑演算
符号学习
神经符号学习
https://daiwz.net
Neural Logical Machine
TensorLog、\(\partial\)ILP 只能 考虑 2 元谓词,而 NLM [Dong et. al., 2020] 对此作出改进:
Expansion
validMove(X,Y) :- movable(X), placeable(Y). %% 维度不匹配 %%% Expansion movableX(X,Z) :- movable(X). placeable(Y,Z) :- placeable(Y). validMove(X,Y) :- movable(X,Y), placeable(Y,X). %% 维度匹配Reduction
movable(X) :- \+isGround(X),\+on(Y,X). %% 维度不匹配 %%% Reduction clear(X) :- \+on(Y,X). movable(X) :- \+isGround(X),clear(Y). %% 维度匹配
符号学习
神经符号学习
https://daiwz.net
Neural Logical Machine
TensorLog、\(\partial\)ILP 只能 考虑 2 元谓词,而 NLM [Dong et. al., 2020] 对此作出改进:
- 以上两种算子将一条规则内的谓词矩阵 \(\mathbf{M}\) 统一成相同维度
符号学习
神经符号学习
https://daiwz.net
神经符号学习
- KBMC
- Embedding 与命题化
- 特殊神经模块
- 混合模型
符号学习
神经符号学习
https://daiwz.net
Memory Network
MemNN [Weston et. al., 2015] 在神经网络中添加 memory 模块
- 记忆体 \(\mathbf{m}\) 拥有多个 slot \(\mathbf{m}_i\)
- \(I\) (Input feature map) 将输入信号转换 \(x\) 为 embedding \(I(x)\)
- \(G\) (Generalisation) 用来更新 \(\mathbf{m}_i=G(\mathbf{m}_i, I(x), \mathbf{m})\)
- \(O\) (Output feature map) 根据输入和记忆体产生输出 \(o=O(I(x),\mathbf{m})\)
- \(R\) (Response) 对输出进行解码 \(r=R(o)\)
符号学习
神经符号学习
https://daiwz.net
NTM 与 DNC
Neural Turing Machine [Graves et. al., 2014] 与 Differential Neural Computer [Graves et. al., 2016] 与 MemNN 类似,通过外部存储和读写头来实现复杂推理。
- \(t\) 时刻的 memory 状态 \(\mathbf{m}^t\)
- 读取结果 \(\mathbf{r}^t=\sum_i w^t_i\mathbf{m}^t_i\),\(\mathbf{w}^t\) 为读取权重
- NTM 不区分读写权重,倾向于对局部进行集中读写,容易覆盖重要内容
- DNC 区分读写,动态地分配读写地址,引入时序管理
符号学习
神经符号学习
https://daiwz.net
NALU
Neural Arithmetic Logic Units [Trask et. al., 2018]
- 动机: 神经网络难以在算数问题上泛化
- 目标: 学习算数函数,例如
- 方案:引入特殊的神经元来近似算数运算
符号学习
神经符号学习
https://daiwz.net
神经排序
Neural Sort [Grover et. al., 2019]
- 动机:排序是一种不可微运算
- 目标:
- 方案:利用排列矩阵 \(P_{\mathbf{z}}\) 来实现可微的近似排序模块
符号学习
神经符号学习
https://daiwz.net
神经符号学习
- KBMC
- Embedding 与命题化
- 特殊神经模块
- 混合模型
符号学习
神经符号学习
https://daiwz.net
两种AI范式
数据驱动的AI
- 以深度神经网络、统计学习为代表的当下主流人工智能;
- 主要通过积累数据(样本)来提升模型性能;
- 直觉、捷径、唯一答案、速度快(System 1);
知识驱动的AI
- 以逻辑推理、专家系统为代表的传统人工智能;
- 主要通过添加符号表达的知识(程序)来提高搜索效率;
- 推理、逐步、允许歧义、速度慢(System 2);
Y. Bengio. From System 1 Deep Learning to System 2 Deep Learning. Keynote at NeurIPS 2018.
符号学习
神经符号学习
https://daiwz.net
符号—神经混合系统
数据驱动与知识驱动互促结合的人工智能系统
符号学习
神经符号学习
https://daiwz.net
DeepProbLog
- 将基于半环的 AProbLog 与神经谓词结合
- ProbLog 部分负责推理、神经网络负责感知
符号学习
神经符号学习
https://daiwz.net
反绎学习(ABL)
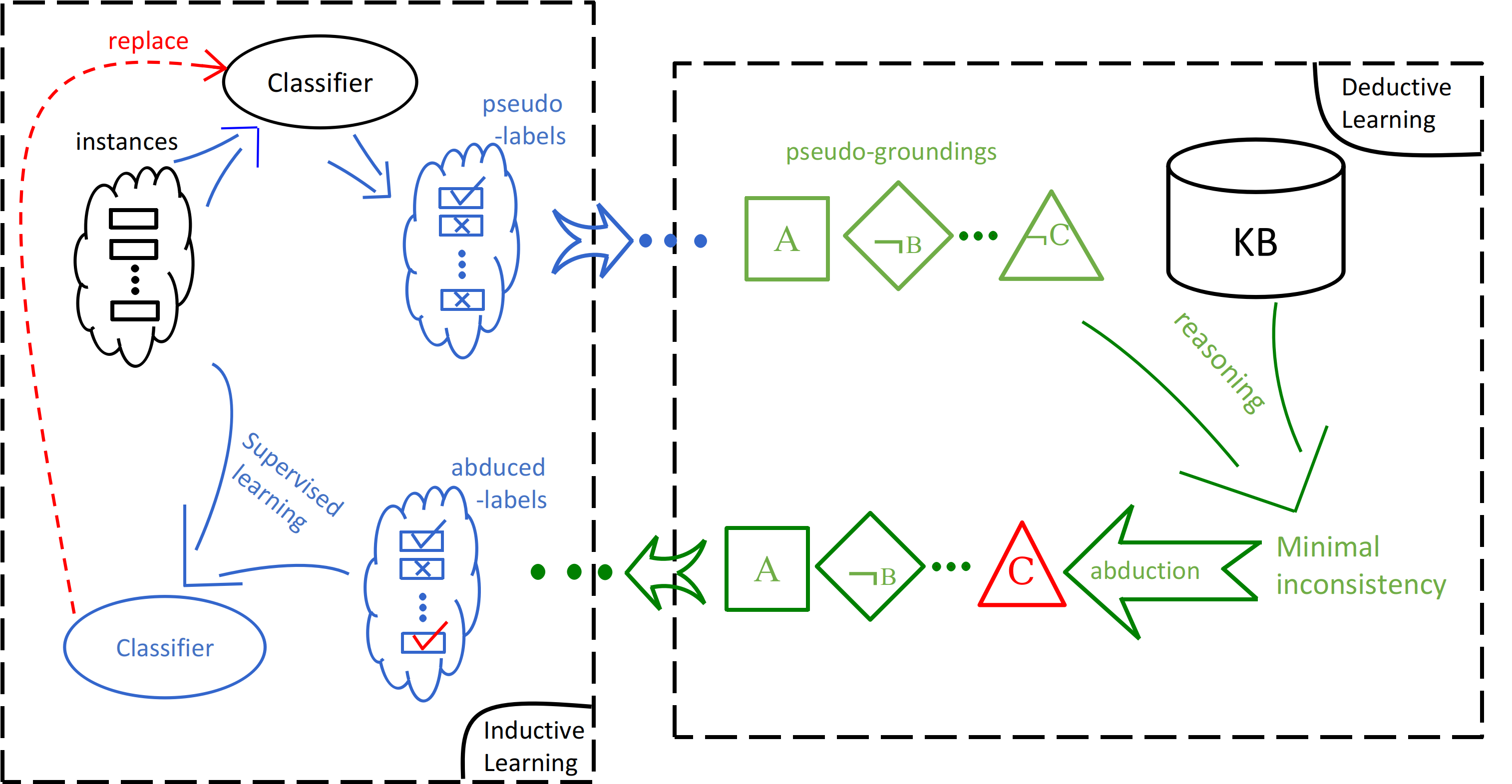
符号学习
神经符号学习
https://daiwz.net
ABL 问题形式化
训练样本:\(\langle x,y\rangle\)
- 机器学习 (例如,神经网络):
\[ z=f(x;\theta)=\text{Sigmoid}(P_\theta(z|x))\]
- 学习一个感知函数:sensory input (\(x\)) ⟶ logic symbols (\(z\));
- (概率)逻辑推理 (例如,(概率)程序):
\[B\cup z\models y\]
- 先验知识(例如,程序、知识图谱) \(B\);
- 推理出最有可能的符号 \(z\) 以训练感知函数令 \(z=f(x)\)
- 优化:最大化 \(z\cup f\) 关于 \(\langle x, y\rangle\) 和 \(B\) 的一致性(例如,后验概率 \(\text{Pr}(z,f\mid x,y,B)\)).
符号学习
神经符号学习
https://daiwz.net
混合模型的主要挑战
W.-Z. Dai, S. H. Muggleton. Abductive Knowledge Induction From Raw Data, IJCAI 2021, accepted.
符号学习
神经符号学习
https://daiwz.net
小结
一代天骄,成吉思汗,只识弯弓射大雕。
俱往矣,数风流人物,还看今朝。