符号学习简介
概率规则学习
(Press ? for help, n and p for next and previous slide)
路径图
符号学习
概率规则学习
https://daiwz.net
概率规则学习
- 参数学习
- 结构学习
符号学习
概率规则学习
https://daiwz.net
参数学习
- \(\theta\):参数,即概率事实、概率规则的权重
- \(\mathcal{D}\):训练数据,\(\{X=x\}^n_{i=1}\)
符号学习
概率规则学习
https://daiwz.net
参数学习
考虑模型 \(M\): \[ \mathrm{Pr}(\theta\mid\mathcal{D},M)=\frac{\mathrm{Pr}(\mathcal{D}\mid \theta,M)\cdot\mathrm{Pr}(\theta\mid M)}{\underbrace{\mathrm{Pr}(\mathcal{D}\mid M)}_{\text{marginal likelihood}}} \]
- 最大似然(ML) \[\theta^*=\mathop{\arg\max}\limits_\theta \mathrm{Pr}(\mathcal{D}\mid\theta,M)\]
- 最大后验概率(MAP) \[\theta^*=\mathop{\arg\max}\limits_\theta \mathrm{Pr}(\theta\mid\mathcal{D},M)\]
- 若 \(\mathrm{Pr}(\theta\mid M)=\text{const.}\),那么 MAP=ML \[\theta^*=\mathop{\arg\max}\limits_\theta \mathrm{Pr}(\theta\mid\mathcal{D},M)=\mathop{\arg\max}\limits_\theta \frac{\mathrm{Pr}(\mathcal{D}\mid\theta,M)\mathrm{Pr}(\theta\mid M)}{\mathrm{Pr}(\mathcal{D}\mid\theta)}=\mathop{\arg\max}\limits_\theta \mathrm{Pr}(\mathcal{D}\mid\theta,M)\]
符号学习
概率规则学习
https://daiwz.net
马尔可夫逻辑的参数估计
\[
\mathrm{Pr}_w(\mathbf{X})=\frac{1}{Z}\prod_i \phi_i (\mathbf{X})=\frac{1}{Z}\exp\left(\sum_i {\color{var(--zenburn-red)}{w_i}} {\color{var(--zenburn-blue)}{n_i }}(\mathbf{X})\right)
\]
符号学习
概率规则学习
https://daiwz.net
马尔可夫逻辑的参数估计
判别式学习:预测条件似然 \(\mathrm{Pr}(y\mid x)\) \[ \mathrm{Pr}(y\mid x)=\frac{1}{Z_x}\exp\left(\sum_{i\in F_Y}w_i n_i (x,y)\right) \]
- \(\color{var(--zenburn-red)}{w_i}\):第 \(i\) 个子句的权重
- \(Z_x\):取值 \(X=x\) 的所有 possible world 权重之和(条件配分函数)
- \(F_Y\):包含问句原子 \(Y\) 的所有子句(马尔可夫毯)
- \(n_i(x,y)\):当变量取值为 \((X,Y)=(x,y)\) 时,第 \(i\) 个子句中为真的原子个数
符号学习
概率规则学习
https://daiwz.net
马尔可夫逻辑的参数估计
生成式学习:预测联合概率似然 \(\mathrm{Pr}(x)\) \[ \mathrm{Pr}_w(X=x)=\frac{1}{Z}\exp\left(\sum_{i\in F} w_i n_i (x)\right) \] 参数 \(w_i\) 关于对数似然函数的梯度 \[ \frac{\partial}{\partial w_i}\log\mathrm{Pr}_w(X=x) = n_i(x) - \sum_{x'}\mathrm{P}_w(X=x')n_i(x') \]
- MCMC 采样,如 WalkSAT
- MAP 估计
符号学习
概率规则学习
https://daiwz.net
马尔可夫逻辑的参数估计

对于含递归规则的一阶概率逻辑问题来说
基于 MCMC (如 Gibbs 采样)的推理基本很难在短时间内收敛
符号学习
概率规则学习
https://daiwz.net
伪似然函数
- \(X_l, l\in\{1,\ldots,n\}\):Markov 网中的所有随机变量(groundings)
- \(MB_x(X_l)\):变量 \(X_l\) 的马尔可夫毯在 \(X=x\) 时的取值
符号学习
概率规则学习
https://daiwz.net
伪似然函数
参数 \(w_i\) 关于对数伪似然函数的梯度
- \(n_i(x_{[X_l=0]})\):在第 \(i\) 个子句中令 \(X=x\) 并强行设置 \(X_l=0\) 时真原子的个数
- 不再需要用 WMC 对全局模型进行推理,速度极快
- 只关心每个 grounding 的局部信息
- 当推理链较长、依赖关系复杂时,准确率非常差
符号学习
概率规则学习
https://daiwz.net
Max-margin Learning
对于判别式学习,除了之间最大化条件对数似然函数,还可以最大化如下“margin”: \[ \frac{\mathrm{Pr}_\mathbf{w}(y|x)}{\mathrm{Pr}_\mathbf{w}(\hat{y}|x)} \]
- 其中 \(\hat{y}\) 是参数 \(\mathbf{w}\) 下随机变量 \(Y\) 除了 \(y\) 以外最可能的赋值: \[\hat{y}=\mathop{\arg\max}\limits_{\bar{y}\in Y\backslash y}\mathrm{Pr}_\mathbf{w}(\bar{y}\mid x)\]
符号学习
概率规则学习
https://daiwz.net
ProbLog 中的参数学习
一阶 ProbLog 的概率分布函数: \[ \mathrm{Pr}(L\mid\mathcal{T})=\prod_{f_n \theta_{n,k}\in L} p_n \prod_{f_n \theta_{n,k}\in L_\mathcal{T}\backslash L} (1-p_n) \] 其中
- \(\{\theta_{n,1},\ldots, \theta_{n,K}\}\) 是第 \(n\) 个一阶概率原子的所有可能变量替换
- \(\mathcal{T}=\mathcal{F}\cup\mathcal{BK}=\{p_1::f_1,\ldots p_N::f_N\}\cup \mathcal{BK}\) 为 ProbLog 程序,其中 \(p_i::f_i\) 为概率原子公式,\(BK\) 是一阶逻辑程序
- 概率原子公式及它们的变量替换定义了一个在其 Herbrand Universe \(L_\mathcal{T}=\{f_1 \theta_{1,1},\ldots, f_1 \theta_{1,K_1},\ldots,f_N \theta_{N,1},\ldots, f_N \theta_{N,K_N}\}\) 上的分布语义
符号学习
概率规则学习
https://daiwz.net
ProbLog 中的参数学习
概率事实 \(\mathcal{F}\)
0.1::burglary.
0.2::earthquake.
0.7::heard(X).
一阶知识库 \(\mathcal{BK}\)
person(mary).
person(john).
alarm :- burglary; earthquake.
calls(X) :- person(X), alarm, heard(X).
\(\mathcal{F}\) 构成的Herbrand Universe 为:
heard(mary), heard(john), burglary, earthquake
符号学习
概率规则学习
https://daiwz.net
ProbLog 中的“解释”
0.1::burglary.
0.2::earthquake.
0.7::heard(X).
person(mary).
person(john).
alarm :- burglary; earthquake.
calls(X) :- person(X), alarm, heard(X).
部分解释(partial interpretation)
\[ \mathrm{Pr}_w((I^+, I^-))=0.1\times 0.7\times(1-0.7)\times\underbrace{(0.2+(1-0.2))}_{\text{earthquake}} \]
符号学习
概率规则学习
https://daiwz.net
LFI-Problog
Learning from Interpretation:
- 从部分或完整观测数据(即证据包含部分/全部 groundings)中学习。
本质上,LFI 是一种最大似然估计:
其中,
- 训练数据 \(\mathcal{D}=\{I_1, \ldots, I_M\}\) 所有 Interpretation 的集合
- \(\theta=\{p_1, p_2, \ldots, p_n\}\) 为所有概率事实的权重
符号学习
概率规则学习
https://daiwz.net
LFI-Problog
当 \(\mathcal{D}\) 中的训练数据均为“完整解释”时:
- 每个 \(I_m\) 中均包含了所有概率事实的真值
- 第 \(n\) 个概率事实 \(p_n::f_n\) 的参数 \(p_n\) 的估计可通过数数来完成
其中,
- \(m\) 代表第 \(m\) 个解释:\(f_n \theta^m_{n,k}\) 是 \(f_n\) 在 \(I_m\) 中利用第 \(k\) 个替换得到的 grounding
- \(Z_n=\sum_{m=1}^M K_n^m\) 是 \(f_n\) 在所有解释中的 grounding 个数
符号学习
概率规则学习
https://daiwz.net
LFI-Problog
- \(I_m\) 中包含隐变量(无真值指派的 groundings)
- 通过 EM 算法求解
其中计算期望的步中需要将 \(I_m\) 编译为 d-DNNF 来推理隐变量的边际概率。
符号学习
概率规则学习
https://daiwz.net
LFI-Problog
符号学习
概率规则学习
https://daiwz.net
LFI-Problog
符号学习
概率规则学习
https://daiwz.net
概率规则学习
- 参数学习
- 结构学习
符号学习
概率规则学习
https://daiwz.net
结构学习的一般框架
- (初始化)精化规则结构;
- 对该规则结构进行参数优化;
- 评估学习质量,例如用测试数据上的 AUC 或 条件对数似然(CLL)对概率逻辑模型打分;
- 如果达到终止条件则输出
- 否则重复步骤1
符号学习
概率规则学习
https://daiwz.net
Beam search
function Markov_Structure_Learning
while beam ≠ ∅
add unit clauses to beam
while beam has changed
for each clause c ∈ beam
c' ← add a literal to c
newClauses ← newClauses ∪ c'
end
beam ← k best clauses in beam ∪ newClauses
end
add best clause in beam to MLN
end
end
符号学习
概率规则学习
https://daiwz.net
Relational Path Finding
- 将常元看作图中的点、谓词看作边
- 多个原子公式的合取看作一条路径
advises(pete, sam), teaches(pete, cs1), tas(sam, cs1).
构成了一条 \((sam,pete,cs1)\) 路径
advises(X, Y), teaches(X, Z), tas(Y, Z).
符号学习
概率规则学习
https://daiwz.net
BUSL
- 利用 relational pathfinding 找到数据中的短路径并泛化
- 将这些路径作为布尔变量 \(\rightarrow\) 马尔可夫网中的节点
- 连接这些节点,形成团簇(cliques)
- 将团簇重构为子句形式
- 对子句打分,并加入模型
符号学习
概率规则学习
https://daiwz.net
BUSL
例如在上面的例子中,可先找到长度小于 2 的短路径
[advises(pete, sam), teaches(pete, cs1)], [tas(sam, cs1)].
符号学习
概率规则学习
https://daiwz.net
利用 Lifting 技术剪枝
Kok and Domingos, ICML’09; ICML’10
- 利用 relational pathfinding 找到 ground paths
- 根据 ground paths 的结构对领域中的常元进行聚类
- 用 random walk 找到图中具有代表性的子结构
- 常见子图
- 对称路径
- …
符号学习
概率规则学习
https://daiwz.net
其他方法
- 利用 ILP 或其他规则学习技术初始化规则结构
- 利用决策树与集成学习同时归纳规则结构和参数
符号学习
概率规则学习
https://daiwz.net
概率规则学习
- 参数学习
- 结构学习
- 题外话
符号学习
概率规则学习
https://daiwz.net
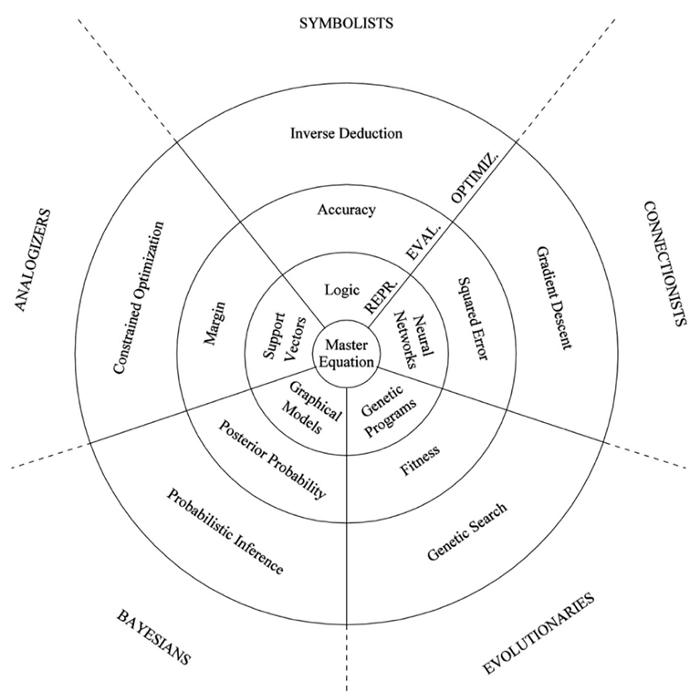
AI 的流派
Pedro Domingos, “The Master Algorithm”