符号学习简介

符号学习简介・一阶逻辑与逻辑程序（下）

Horn子句

至多只有一个肯定文字的子句 \[H\vee \neg B_1 \vee\neg B_2 \vee\cdots\vee \neg B_n=H\leftarrow B_1 \wedge B_2 \wedge\cdots\wedge B_n\] 其中\(H\)和\(B_i\)均为原子公式

Prolog规则

在逻辑程序（Programming with Logic, Prolog）中，我们用：

• ":-"（“colon dash”）代替“\(\leftarrow\)”
• ","代替“\(\wedge\)”
• "."代表句子完结

Prolog中的推理

1. 归结（resolution）
2. 线性归结（linear resolution）
3. 选择线性归结（selective linear resolution, SL-resolution）
4. 定子句上的选择线性归结（SLD-resolution）

归结原理

其中：

• \(\color{#CC9393}{L_i}\)与\(\color{#8CD0D3}{M_j}\)谓词相同、符号相反
• \(\theta\)是\(\color{#CC9393}{L_i}\)与\(\neg\color{#8CD0D3}{M_j}\)的最大一般合一化子（Most General Unifier, MGU）
• 经过替换后的\(\color{#CC9393}{L_i}\theta\)与\(\neg\color{#8CD0D3}{M_j}\theta\)为互补（complement）文字
• 横线下面的部分被称为归结商（resolvent）

归结原理

归结定理（Resolution Theorem）： 若\(S\)是任意有穷子句集，那么\(S\)是不可满足的当且仅当\(\mathfrak{R}^n(S)\)中包含空子句，其中\(\mathfrak{R}^n(S)\)是对\(S\)中的子句连续做\(n\)次归结后的结果。

归结反驳（Resolution refutation）：“反证法” \[\Gamma\vdash A \Leftrightarrow \Gamma, \neg A\vdash \square\]

归结原理

例子：一个有结合律的乘法系统中，若左乘和右乘均有解，那么这个系统中至少存在一个右单位元。

线性归结

线性归结（Linear Resolution）：子句集合\(S\)的一个线性归结\(D\)是一个序列\((C_1, \ldots,C_n)\)，使得\(C_1 \in S\)且\(C_{i+1}\)是\(C_i\)与\(B\)的归结商，其中要么：

• \(B\in S\)，或者
• \(B=C_j\)是\(C_i\)的祖先，且\(j < i\)

线性归结

线性归结的搜索空间非常大：\(S=\{P\vee Q, \neg P, \neg Q\vee R, \neg R\vee S, \neg R\vee \neg S\vee T, P\vee \neg T\}\)

选择线性归结

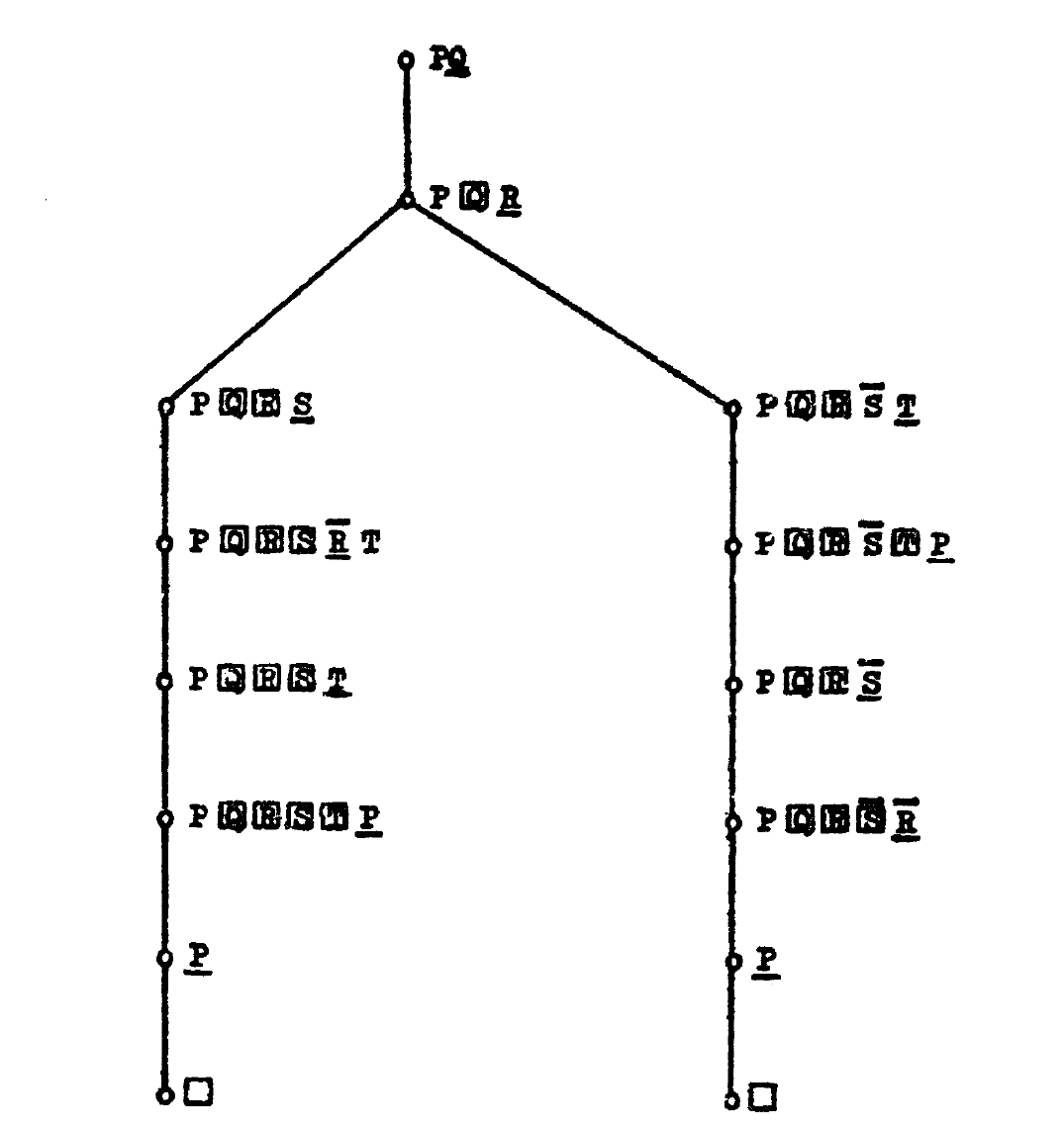
选择线性归结（Selective Linear Resolution）在线性归结的基础上添加了选择函数（selection function），每次只选择一个文字进行归结

例如，依然对于\(S=\{PQ, \bar{P},\bar{Q}R, \bar{R}S, \bar{R}\bar{S}T, P\bar{T}\}\)

定子句的选择线性归结

Demo:

% Facts
mother(ann,amy).
mother(ann,andy).
mother(amy,amelia).
mother(linda,gavin).
father(steve,amy).
father(steve,andy).
father(gavin,amelia).
father(andy,spongebob).
% Rules
parent(X,Y) :- father(X,Y).
parent(X,Y) :- mother(X,Y).
grandparent(X,Y) :- parent(X,Z), parent(Z,Y).
% Query
?- grandparent(ann, spongebob).

SLD-归结

SLD-归结

SLD-推导（SLD-derivation）：若\(\mathrm{P}\)是一个逻辑程序且\(G\)是一个目标子句。\(\mathrm{P}\cup \{G\}\)的一个SLD-推导由以下部分组成：

• 一个目标子句序列（可能无穷）\(G_0=G,G_1,\ldots\)
• 一个程序规则序列\(C_1, \ldots C_2, \ldots\)
• 一个MGU序列\(\theta_1, \theta_2, \ldots\)

使得\(G_{i+1}\)是由\(G_i\)与\(C_{i+1}\)通过\(\theta_{i+1}\)推导而来。

SLD-归结的答案

计算答案（computed answer）：若\(\mathrm{P}\)是一个逻辑程序且\(G\)是一个目标子句。\(\mathrm{P}\cup \{G\}\)的一个计算答案是一个\(G\)上的变元替换\(\theta\)，它是由SLD-反驳过程中使用的所有MGU序列复合而来。

mother(ann,amy).      father(steve,amy).
mother(ann,andy).     father(steve,andy).
mother(amy,amelia).   father(gavin,amelia).
mother(linda,gavin).  father(andy,spongebob).

parent(X,Y) :- father(X,Y).
parent(X,Y) :- mother(X,Y).
grandparent(X,Y) :- parent(X,Z), parent(Z,Y).

?- grandparent(ann, A), grandparent(linda, A).
% A = amelia

SLD-归结的有效性

定理：若\(\mathrm{P}\)是一个逻辑程序且\(G\)是一个目标子句。那么所有通过SLD-反驳计算得出的答案\(\theta\)都是正确答案，即\(\forall(G)\theta\)是\(\mathrm{P}\)的逻辑推论（\(\mathrm{P}\models G\theta\)）。

符号学习简介・一阶逻辑与逻辑程序（下）

逻辑程序的语义

例如，对于以下逻辑程序\(\mathrm{P}\)

p(X) :- q(f(X), g(X)).
r(a).

它的埃尔布朗域\(\mathrm{U_P}\)为

a, f(a), g(a), f(f(a)), f(g(a)), g(f(a)), g(g(a)), ...

逻辑程序的语义

例如，对于以下逻辑程序\(\mathrm{P}\)

p(X) :- q(f(X), g(X)).
r(a).

它的埃尔布朗基\(\mathrm{B_P}\)为

p(a). q(a,a). r(a). p(f(a)). p(g(a)). q(f(a),f(a)). q(f(a),g(a)). ...

逻辑程序的语义

例如，对于以下逻辑程序\(\mathrm{P}\)

p(X) :- q(f(X), g(X)).
r(a).

它的两个埃尔布朗模型为

MP1 = r(a), p(a), q(f(a),g(a)).
MP2 = r(a).

最小埃尔布朗模型

最小埃尔布朗模型

最小埃尔布朗模型的计算

只要找到最小不动点，就能找到逻辑程序的模型

mother(ann,amy).   mother(ann,andy).   ...
father(steve,amy). father(steve,andy). ...
% Rules
parent(X,Y) :- father(X,Y).
parent(X,Y) :- mother(X,Y).
ancestor(X,Y) :- parent(X,Y).
ancestor(X,Y) :- parent(X,Z), ancestor(Z,Y).

直接推论\(\mathrm{T_P}^n\) （有可能无穷）

1: [parent(steve,amy), ..., parent(linda,gavin)]
2: [parent(steve,amy), ..., parent(linda,gavin),
    ancestor(steve,amy), ..., ancestor(linda,gavin)]
3: [parent(steve,amy), ..., parent(linda,gavin),
    ancestor(steve,amy), ..., ancestor(linda,gavin),
    ancestor(steve,amelia, ..., ancestor(linda,amelia))]
4+: no change.

SLD-归结的完备性

通过SLD-归结推理出来的结果 vs \(\mathrm{T_P}\)计算出来的结果

可行原子集合（success set）若\(\mathrm{P}\)是一个逻辑程序，它的可行原子集合为： \[\{A\mid \text{$\forall A\in \mathrm{B_P}$使得$\mathrm{P}\cup \{\leftarrow A\}$有一个SLD-反驳}\}\]

SLD-归结的完备性

符号学习简介・一阶逻辑与逻辑程序（下）

元解释器

为什么是Prolog？

1. Prolog是一种同像性（homoiconic）语言
   • Prolog程序就是Prolog terms
2. Prolog有许多解释器能利用的隐式功能
   • 基于SLD-归结的深度优先搜索
3. Prolog语句非常简单
   • Head :- Body

元调用（Meta-call）

若我们有一个程序，

natnum(0).
natnum(s(X)) :-
    natnum(X).

Prolog能够动态地运行它：

?- Goal = natnum(X), call(Goal).
Goal = natnum(0), X = 0 ;
Goal = natnum(s(0)), X = s(0) ;
Goal = natnum(s(s(0))), X = s(s(0)) ;
Goal = natnum(s(s(s(0)))), X = s(s(s(0))) ;
Goal = natnum(s(s(s(s(0))))), X = s(s(s(s(0)))) ;
...

自我解析

也叫做自省（reflection and introspection）

若我们有一个程序，

:- dynamic complicated_clause/1. % 需要声明这是公共谓词

complicated_clause(A) :-
    goal1(A),
    goal2(A),
    goal3(A).
complicated_clause(1).

Prolog能够用clause/2解析它：

?- clause(complicated_clause(Z), Body).
Body =  (goal1(Z), goal2(Z), goal3(Z)) ;
Z = 1, Body = true.

最基础的元解释器

通过meta-call和clause/2实现SLD-归结：

prove(true).
prove((A,B)) :-
    prove(A),
    prove(B).
prove(Goal) :-
    Goal \= true,
    Goal \= (_,_),
    clause(Goal, Body),
    prove(Body).

用在natnum/1中：

?- prove(natnum(X)).
X = 0 ;
X = s(0) ;
X = s(s(0)) ;
... .

最基础的元解释器

通过meta-call和clause/2实现SLD-归结：

prove(true).
prove((A,B)) :-
    prove(A),
    prove(B).
prove(Goal) :-
    Goal \= true,
    Goal \= (_,_),
    clause(Goal, Body),
    prove(Body).

解释不了自己：

?- prove(prove(natnum(X))).
ERROR: No permission to access private_procedure `(\=)/2'

自定义语法

比如，新定义一个谓词head_body(Head, Goals)

head_body(natnum(0), []).
head_body(natnum(s(X)), [natnum(X)]).

新的SLD-归结元解释器：

prove([]).
prove([G|Gs]) :-
    head_body(G, Goals),
    prove(Goals),
    prove(Gs).

自定义语法2

利用list difference定义谓词head_body(Head, Goals0, Goals)

• Head成立当且仅当Goals0-Goals成立

head_body(natnum(0), Rs, Rs).
head_body(natnum(s(X)), [natnum(X)|Rs], Rs).

新的SLD-归结元解释器：

prove([]).
prove([G|Gs]) :-
    head_body(G, Goals, Gs),
    prove(Goals).

解释解释器的解释器

prove/1可以表达为：

head_body(prove([]),Rs,Rs).
head_body(prove([G|Gs]),[head_body(G,Goals,Gs),prove(Goals)|Rs], Rs).

head_body/3自己也可以表达为：

head_body(head_body(Head,Goals0,Goals), Rs, Rs) :-
    head_body(Head, Goals0, Goals).

解释解释器的解释器

% Meta-Interpreter
prove([]).
prove([G|Gs]) :-
    head_body(G, Goals, Gs),
    prove(Goals).

head_body(prove([]),Rs,Rs).
head_body(prove([G|Gs]),[head_body(G,Goals,Gs),prove(Goals)|Rs],Rs).

head_body(head_body(Head,Goals0,Goals), Rs, Rs) :-
    head_body(Head, Goals0, Goals).

% Program
head_body(natnum(0), Rs, Rs).
head_body(natnum(s(X)), [natnum(X)|Rs], Rs).

?- prove([prove([natnum(X)])]).
X = 0 ;
X = s(0) ;
X = s(s(0)) ;
X = s(s(s(0))) ;
... .

小结

逻辑程序部分的小结

1. 逻辑程序（definite program）的组成：
   • 规则（Horn clause）
   • 事实（unit clause）
2. 归结原理与SLD-归结
   • 问句（goal clause）
   • 反驳（refutation）
3. SLD-归结的有效性与完备性
4. SLD-归结的实现

课后练习

考虑一个上下文无关语言（context-free language）\(a^n b^m\)（可以使用Prolog list，如[a,a,a,b,b,b,b]表示），其中\(n\geq0\wedge m\geq 0\)。回答以下问题，并解释你的做法：

• 写一个逻辑程序来描述该语言，令符合语法的X有anbm(X)为true
• 写一个meta-interpreter可以解析上下文无关文法
  • 提示：能够解释有限状态自动机的meta-interpreter
• 列出接受\(a^n b^m\)时你的meta-interpreter所需的知识
  • 提示：与语法相关的自动机状态与状态转移操作

Deadline：4月15日23:59

课后练习要求

1. 环境：SWI-Prolog 或 Scryer Prolog
2. Prolog 教程
   • Learn Prolog Now
   • SWI-Prolog Manual
   • The Power of Prolog
     • Meta-Interpreters